
今日は「開成」と「麻布」の算数の入試問題から見た教育の違いに関する記事です。
記事はこちらになります

特殊算が出る学校、出ない学校
実際、中学受験校のすべてで特珠算が出題されるわけではない。開成や駒場東邦、神奈川県の聖光学院では、ほとんど出題されない。その一方で麻布や女子学院、京都の洛星や灘の入試では定番だ。それも、いわゆるつるかめ算と旅人算などの特珠算を組み合わせた、より高度な特珠算が出題されている。
中学受験を経験していない私にとって、子供の中学受験を通して初めて「特殊算」というものに触れました。
「特殊算」の種類が何種類あるのかは分かりませんが、頭を使って工夫する解き方をする必要があるので「小学生らしい解き方だな」と感じます。
ただ、中学入試がかなり高度化している昨今、難関校をはじめとして、特殊算そのものがストレートに問われるケースは減っているようです。
というのも、① 特殊算単体で問題を難しくするのには限界がある、② ①の結果、仮に出題しても差がつかない、という事情があるからです。
つまり、中学の学習に耐えられる計算力の速さ、抽象的な思考力を鍛えようとする開成型の教育には、つるかめ算などの特珠算はそれほど重要なものではない。一方で「いかに」「幾通りもの解法」を考えさせ、いわば仮定を立てさせることで具体的なイメージを促す麻布型の教育では、特珠算は必要だと考えられている。
実際、今年(2021年)の麻布の入試でどのような問題が出たかを見てみます。

途中で速さが変わっているので、一瞬「速さのつるかめ算か」と思いきや、「速さと比」の問題でした。(都合により線分図は省略していますが)実際には線分図を描いて、問題文の情報を線分図上に集約することが出発点になります。
(1)は比較的簡単で、スタート → 地点Pまでの距離が3.6km、地点P → ゴールまでの距離が2.4kmとわかるので、たかし君のスタート → Pの速さを②、P → ゴールまでの速さを①などとして時間の比をとると、(3.6/2):(2.4/1)=1.8:2.4=3:4となります。
つまり、たかし君のかかった時間の比(スタート → 地点P:地点P → ゴール)=3:4ということです。
たかし君は40分かかってゴールしているので、スタート → 地点Pまでかかった時間は40分×[3/(3+4)]=120/7分。3.6kmを120/7分で進んでいるので、速さ=3600m÷120/7=210m/分
(2)次にまこと君に注目します。まこと君が速さを2.5倍に変えたのは、120/7分+15分=225/7分後とわかります。一方、たかし君の後半の速さは210m/分÷2=105/m分なので、まこと君がたかし君を追い越したのは、40分ー(600m÷105m/分)=40ー40/7=240/7分後です。
結局、まこと君は(6000-600=)5400mを225/7分で走り、速さを変えたのが240/7分後なので、速さを変えて(2.5倍の速さで)走った時間は240/7-225/7=15/7分となります。
ここまで来れば後はどのように解いても良いのですが、最初の速さを②、変更後の速さを⑤として、225/7×②+15/7×⑤=5400m ⇔ 450/7+75/7=525/7=5400m。 ②=5400÷525/7×2=144m/分。
よって、(1)210m/分、(2)144m/分となります。
小6の模試などに出てきそうな問題ですが、分数計算が絡むので計算が少し大変です。限られた時間内にミスなく解ききるには、普段から相当の練習量が必要になるでしょう。
中学数学を学ぶための確かな計算力を要求していると言えるのではないでしょうか。
次の問題です。

これはどうやって解くのでしょうね?
とりあえず、問題文を式で表してみます。もうこの辺りの思考からして、中学生並のレベルが要求されているように思います。
カードA,カードBの枚数をぞれぞれA枚、B枚とすると、A+B=32(枚)…①
0.07×A+0.13B=〇〇.78(整数部分の〇〇は不明)…②
のような形になるということです。
整数部分はとりあえず無視して、小数部分に注目するのがポイントです。
②の両辺を100倍して(小数点を消すと)、7×A+13×B=〇〇78…②´
相変わらず〇〇が何かは分からないのですが、仮にAが32枚あったすると、7×32=224、仮にBが32枚あったとすると、13×32=416。
ということは、216≦「〇〇78」≦416より、〇〇78は3桁の数となり、278か378のいずれかということになります。
一旦整数部分は忘れて小数部分だけに注目し、つるかめ算的な発想を使って範囲を絞るのがポイントですね。
あとは、2つの場合に分けて、消去算で解けばよいわけです。
(場合1) A+B=32 7×A+13×B=278
(場合2) A+B=32 7×A+13×B=378
(場合1) A=23 B=9 (場合2)整数解なし
よってA=23枚、B=9枚。
ただし、これが答えではなく、求めるのは整数部分なので、1.07×23+2.13×9=43.78 よって、整数部分は43
数の性質、場合分け、消去算が組み合わさっていますから、これは結構大変です。
高校入試で出しても正答率は結構低くなるのではないでしょうか。
最後は5番。
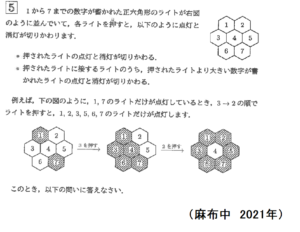
難関校が好きそうな見るからに面倒臭そうな試行錯誤系問題。
小問が3問ありますが、(1)と(2)は試験時間内に何とかなりそうですが、(3)は押す回数が5回もあるので、実際の試験では後回しでしょうね。
開成型? 麻布型? → むしろ難関校型では?
2022年には高等学校の教科書も変わる。前回でも触れたように、2021年度の大学「共通テスト」は思考力・判断力・表現力を求めるものにシフトしてきている。 こうした大学の受験の変化を見据えて考えてみると、はたして早い時期から高い抽象性を獲得させ、高速計算力を高めることが重要なのか。それとも多様な思考力をじっくり育てていくことを大切にしたほうがいいのか。どちらが子どもの発育歴に沿っているものであり、のちのち優れた生徒を育てることにつながっていくのか。 それを考えると、小手先だけではなく、物事をしっかり考えるという「地頭」(じあたま)を鍛えることへの模索は、こうした中等教育の教育観を問う意味で重い。 いまの世界および日本の状況を眺めてみると、親として、受験名門校、いい会社、高い収入といった〝鉄板の方程式〟に最短距離で子どもを導くのがいいとされてきた時代は、そろそろ終焉に近い印象だ。その意味で、一見、無用の算数のように思える特珠算の出題には、いろいろ体験し、冒険してもいいじゃないかという教育の可能性を示すものかもしれない。
私自身は中学受験の専門家でもなく、難関校の算数問題を入念に検討した経験はないのですが、最近の難関校の入試算数問題を見ると、「ある手掛かりをもとに、試行錯誤しながら粘り強く課題に取り組む生徒」を欲しているように思います。
そのような生徒を選別するために、かつての牧歌的な「特殊算」の問題はほとんど出なくなり、代わりに「整数(規則性・数の性質)」や「場合の数」の出題が目立ちます。そして、これに試行錯誤系というか作業量を伴う問題が良く出題される印象があります。
記事にある開成・麻布・武蔵・駒場東邦・聖光学院といった難関校は、上記のような問題を好んで出している感じですね。その点では、素人目から見て差は感じません。
もともと素質のある生徒を早い段階で選抜して鍛えるわけですから、「そりゃ、進学実績も上がるわな」という感じです。
ところで、昨今の中学受験で懸念されるのは、選抜(選別)が早まっているが故に、むしろ「早い段階で可能性を閉ざしてしまっているのではないか」ということです。
「(塾で習う算数が難しくて点数が上がらないから)算数が苦手。数学も多分苦手。」みたいな…。 🙁
塾などでは非常に難しい内容を勉強しているので、そんなに簡単に解けるようになったり、高得点(高偏差値)は取れませんから。
「数十年前の小学6年生の私」が今年の麻布中学の算数の入試問題を解いたら…多分0点でしょうね。 😛
中学受験生の皆さん、自信を持ちましょう!!


