
今回と次回で2回にわたって、過去に出題された中学入試問題を例に、高校数学との関連などについて、勝手に考察したいと思います。
高校数学レベルも出題される中学受験算数
「中学受験」において、算数の学習は極めて重要です。
しかし、受験算数というのは非常に難しい。
「受験算数」で何を勉強しているかと言うと、別に算数自体を極めるような勉強をしているわけではなく、かなりの部分は中学以降で学ぶ数学の先取りになっています。
例えば、中高一貫校で使用される割合が高い 体系数学などを見れば明らかですが、受験算数によってかなりの範囲は既習内容となっています。
しかしこれで済まなくなってきているのが昨今の中学受験。
受験生のレベルが年々上がってきている(=塾での対策が進んでいる)ことから、中学レベル数学に飽き足らず、「高校数学領域に入り込んできている」というのが実情です。
このことは過去の記事でも指摘したとおりであり、出題される高校数学の分野の例としては「場合の数」と「整数」になります。
これらの領域は、本来であれば高校の数学Aで本格的に学ぶ内容となりますが、事前準備や約束事が比較的少ないので、難関中学を中心に出題されるケースが目立っています。
ということで、今回は「場合の数」の例をとりあげつつ、「中学校がどのような力を見ようとしているのか」という点を考察してみたいと思います。
場合の数(ラ・サール中学 2019年)
①から⑦までの番号のついた座席が横1列に並んでいます。
① ② ③ ④ ⑤ ⑥ ⑦
人が座っている席のとなりには誰も座らないとします。
たとえば、①の席に人が座った場合②には誰も座らず、②の席に人が座った場合
①と③には誰も座りません。このとき、次の問に答えなさい。
(1)A、B、C、D4人の座り方は何通りですか。
(2)A、B2人の座り方は何通りですか。
(3)A、B、C3人の座り方は何通りですか。 (ラ・サール中学校 2019年度)
図や絵を描いてイメージする
まず(1)ですが、「問題文が何を言っているか」を把握する必要があります。
この問題は比較的分かり易いのですが、中には一読しただけでは「何のことなのかさっぱり…」という問題もあります。
こういう場合には、問題文を何度か読んだり、重要な情報に線を引いたり、自分で図に書いたり、小さい数で試したりして、問題文の趣旨を把握することが大事です。
この問題も、文章を読んだだけではよく分からないので、自分で実際に図や絵を描いてイメージすることが大切です。
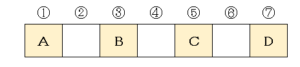
勘が良いお子さんならここで気づきますが、念のためもう少し描いてみます。
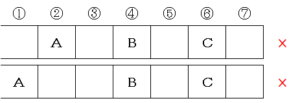
…と、この辺まで描いてみると、A,B、C、Dがとなり合わない座り方は、最初に書いた1パターンしかないことが確認できます。

あとはA,B,C,Dの順番を入れ替えて考えれば良いので、「4人の並べ方(=順列)と同じことだ」と気が付けば簡単です。
答えは、4×3×2×1=24通りとなります。
1パターンしかないので、「順列の基本」と結びつけやすい問題だと思います。
なお、高校数学ではP(Permutation)やC(Combination)の頭文字を使って、4P4などと公式を使うのですが、こうした公式を小学生に教える塾もあるようです。
色々な教え方があるとは思いますが、個人的にはかなり疑問を感じます。
「①にはA~Dの4人が座る可能性があるから4通り、③に座るのは①に座った残り3人だから3通り、⑤には残り2人だから2通り、⑦は残った一人に自動的に決まる。」というように、しっかりとロジックを押さえておけば、(少なくとも中学受験レベルでは)公式は不要だと思います。
樹形図を使った書き出しと典型論点の融合
(2)も最初は図を描いて考えます。これもいくつか書き出してみます。
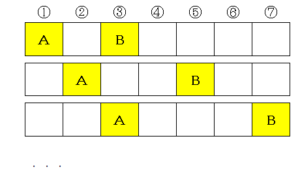
いくつか書き出してみると、結構沢山ありそうなことが分かります。全部書き出すにしても、行き当たりばったりの方法では、数え漏れや重複が出そうです。
そこで、(ⅰ)規則的に書き出す、(ⅱ)視点を変える、のいずれかの方針を検討します。
こうした発想ができるということが、実は問題に正解できるかどうかということより重要だったりします。
(ⅱ)は、制限時間のある入学試験ではなかなか難しいので、ここでは規則的に書き出す方法を採用します。「書き出し ➡ 樹形図」です。「場合の数」の難問は、この「書き出し」がポイントになるケースが多いので、樹形図は非常に重要です。
規則的に書き出すためにA,Bのどちらかを固定します。A,B両方を同時に動かすとわけがわからなくるので、「一方固定」するのが常道です。
ここでは、Aを固定して以下のように(左から右へ)秩序正しく書き出します。

書き出すと15通りとなりますが、答えは15通りではありません。
AとBを入れ替えた座り方もあるので、「×2」が必要で、15×2=30通りとなります。
この「×2」をするというのは、例えば「家族の集合写真を撮る際の並び方の問題」で、父と母が並ぶ場合に父と母の位置が入れ替わる場合がある(×2をする)という典型題などでもお馴染みの論点です。これを思い出せるかどうかが、この問題のもう一つのポイントでしょう。
(慣れてくると)書き出しながら「AとBを入れ替える場合もあるから、最後に×2をする必要があるな」ということが思い浮かぶようになります。解いている途中で解答ゴールが見えるようになると、自信を持って、かつ、楽に問題を解き進めることができます。
さらに、解き始めた段階で「この問題は樹形図で整理して、最後に『×2』だな」というように解答方針がサッと頭に浮かぶようになると、相当力がついていると思います。
(3)も(2)と同様にいくつか書き出してみます。
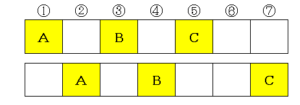
(1)、(2)を通じて問題の意味合いが分かっていれば、わざわざ例を書き出さなくても、いきなり樹形図を描いても良いでしょう。
ここでも秩序正しく丁寧に書き出すことがポイントです。

答えは10通りではありません。
A,B,C3人の並び替えが、3×2×1=6通りあることを忘れないようにします。これも慣れると、書き出し途中で並び替えの必要性に気づく(※)ようになります。
よって、10×6=60通り
| (※)例えば、「3の倍数の個数を求める問題」(典型題)では、 ① 各位の数の和が3の倍数になるような数の組み合わせを作る. ② 各位の数を並べ替える. といった解答手順になりますが、上記のA,B,Cの並べ替えは②の手順と同じです。 |
初めて見た問題であっても、①題意をしっかり掴み、②丁寧に秩序正しく書き出し、③既知の論点(2人の入れ替え、3人の並び替え)と組み合わせることで、十分正解できる問題と言えるでしょう。
この問題を通じて、中学校が受験生に求めている力は以下の3つだと思われます。
② 規則正しく書き出す力 ⇒ 作業力
③ 基本事項(順列や組合せの基本)と問題とを結びつける力
次回は別解を考えるとともに、(高校)数学の本質的な勉強なども考えたいと思います。




