はじめに
このブログで何度か指摘しているとおり、難関校といわれる中学の入試算数は高校数学の領域まで入り込んでいます。
具体的には、数学Aの「整数」・「場合の数」(確率を除く)・「図形」及び数学Bの「数列」あたりがその範囲として挙げられます。
とりわけ、「整数」は小学生で小数や分数の概念が登場する前に、一通り加減乗除計算ができるようになることからも、非常に身近です。
また、マスター・オブ・整数―大学への数学の以下の記述を読むと、「難関校がなぜ好んで整数問題を出題するか」という背景の一端が分かります。
数学には、特定の約束事を学習しないと、問題を全く解けない分野があります。たとえば、積分を習ったことのない人が、∫の記号のついた計算はできません。(中略)これに対して、整数の問題の大半は、かなり難しい問題でさえ、中学校卒業程度の知識があれば、十分取りくむことができます。整数問題の難しさは、「長大な約束事を理解しなければならない難しさ」ではなく、「自力で工夫し、考えぬかねばならない難しさ」なのです。
(栗田哲也 福田邦彦著 「マスター・オブ・整数」 東京出版 『本書の利用法』より)
灘中 2021年入試より
今回とりあげるのは、以下の「灘中 2021年 1日目」の整数問題です。
Aは2桁の整数で、A×Aを15で割ると1余ります。このような整数Aは全部で□個あります。(灘中 2021年 1日目 5⃣)
ご存じの方も多いと思いますが、灘中は2日間にわたって入試が行われ、1日目の算数は主として一行題が、2日目の算数では文章題が出題されます。
「首都圏難関校でも(灘中で出題された)何年か後に類題が出題される」などということが言われていたりしますが、進学塾だけでなく、多くの中高一貫校が灘中の入試問題には注目していると言えるでしょう。
なお、一行題と言っても、中学受験塾の模試の前半に出てくるような易し目の問題ではなく、今回取り上げる問題のように、相当難度が高い問題が目白押しです。
それでも、今年(2021年)の入試結果を見ると、1日目の算数の合格者平均は83点とかなりの高得点で、例年に比べると大分易しかった(但し、灘中比)ようです。
2日目は合格者平均点が60点台と難しくなりますが、(2日間の)算数で200点(満点)をとった受験生がいたのは驚異的と言わざるを得ません。
前置きはこのくらいにして、早速問題を見ていきます。
<解法1> 15で割った余りの規則性の問題として解く
問題を再掲します。
Aは2桁の整数で、A×Aを15で割ると1余ります。このような整数Aは全部で□個あります。(灘中 2021年 1日目 5⃣)
「15で割り切れる数は何個?」という問題であれば非常に簡単なのですが、「余り」があるのが厄介です。
パッと思いつくこととして、Aは2桁の整数なので、10~99まで90個の候補があります。
1つずつ90回試せば答えは出ますが、そんな時間はないので何かしらの「規則性」を見つける必要があります。
端的には、15で割った時の余りの規則性に気付けるかということになります。
整数の分類
一般に、整数は偶数と奇数に分けられますが、この分類は「(整数を)2で割った時の余り」に基づく分類といえます。また、「整数を3で割った時のあまり」によって3×□,3×□+1,3×□+2(□は整数)などと表して議論を進めていく方法も中学受験では時々見かけます。
数学(中学 or 高校?)では、以下のようなことを習います。
| 整数Aを整数bで割った時の商をm、余りをnとすると、A=bm+n(0≦n<b) |
言われてみれば当たり前の式で、「余り<商」になることは小学生でもわかります。しかし、この関係を使うとすべての整数が表せるということまでは案外気づかないかもしれません。
すべての整数をこの関係を使って表せるからこそ、本問を解く場合、15で割った余りに注目して(代表値を前提に)、安心して議論を進めることができるという流れになると思います。
余りに注目するという考え方は、中学受験などでも出てくる「カレンダーの曜日を7で割った時の余りと対応させる問題」などでもお馴染みですが、意外に奥が深いテーマで、自在に使いこなすのは(一般に)高校生以上になると思います。
15で割った余りで分類 → 規則性発見
整数を15で割った時のあまりを基準に(整数が)分類できるということに気づけば、余り0から余り14までの15個について調べていくことで、規則性を見つけられるのではないかという推測が成り立ちます。
実際にはそこまでの深い考えはなく、「とりあえず小さい数から試してみよう」という程度でも構いません。
1×1=1 → あまり 1 〇
2×2=4 → あまり 4
3×3=9 → あまり 9
4×4=16 → あまり 1 〇
5×5=25 → あまり10
6×6=36 → あまり 6
7×7=49 → あまり 4
8×8=64 → あまり 4
9×9=81 → あまり 6
10×10=100 → あまり10
11×11=121 → あまり 1 〇
12×12=144 → あまり 9
13×13=169 → あまり 4
14×14=196 → あまり 1 〇
15×15=225 → あまり 0
==================
(16×16=256 → あまり 1 〇)
…
やっていること自体は簡単ですが、地道な作業が必要になる点がポイントです。
さらに、15個周期(=15で割った余りで分類)という意識があやふやだと、「あれ~、(いくつ飛びとかじゃないから)規則性が見つからないな~」、とか、「条件を満たすのは、1の位が1と4のときの2個だから…、2×9=18個だ」などといったことになりかねません。
特に、後者はいつの間にか1~10の10個周期になってしまっているわけですが、「15で割ったのだから15個周期」という点を明確に意識していないと、(慣れている)10のカタマリに引きずられてしまいます。
数学が得意な方はそういうことはないのでしょうが、私のような「文系人間」は、注意しないとこうしたトラップに容易に引っかかってしまう可能性があります。
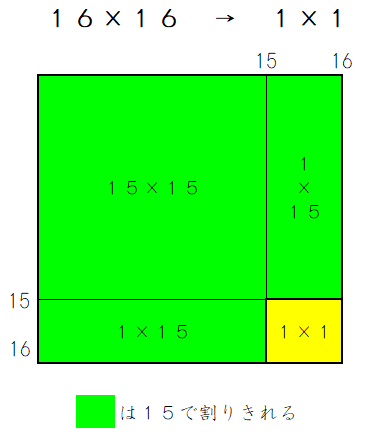
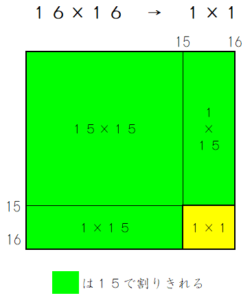
なお、16×16は、以下の図からも分かる通り、15で割った時の余りという点では「16×16」と「1×1」は同じであることから、これ以上調べる必要がないことが分かります。
解答への道
算数を利用した解法だと、15個周期の中で余りが1となるパターンを4パターンに分けて
「1×1」パターン:16×16 31×31 46×46 61×61 76×76 91×91 → 6個
「4×4」パターン:19×19 34×34 49×49 64×64 79×79 94×94 → 6個
「11×11」パターン:11×11 26×26 41×41 56×56 71×71 86×86 → 6個
「14×14」パターン:14×14 29×29 43×43 58×58 73×73 88×88 → 6個
で、6×4=24個となるでしょうか。
一方、高校数学を使うともう少し見通しが良くなります。
例えば今回の整数(A)を15で割った時の商(m)と余り(n)を使って、A=15m+nなどと表します。なお、10 ≦ 15m+n ≦99(0≦n≦14)
また、A2=(15m+n)2=152m2+2・15mn+n2=15(15m2+2mn)+n2=15×□+n2と表せることから、A2を15で割った時の余りはn2だけに注目すれば良いことが明確に分かります。
後は注意深く数えれば良いのですが、15m+n≦99より、0≦m≦6、n=0,1,2,…、14を代入して、n2を15で割った時の余りを書き出します(前掲の表参照)。
m=1からm=5の時は、フルセットの組があるので、4×5=20個
一方、m=0のときは(11×11と14×14の)2個、m=6の時は、(91×91と94×94の)2個で、合計24個と求めることができます。
<解法2> 素因数分解を用いる方法
15=3×5から、「素因数分解をすればよいのでは?」と思いつく小学生もいるでしょう。
とても良い視点です。
その先どう進めるかはなかなか思いつかないかもしれませんが、色々考えて試してみることが、問題に正解する以上に重要だと思います。
「15で割ると1余る」の言い換え
「15で割って1あまる」ということは、「3で割っても1あまり、5で割っても1あまる」と同じ意味です。小学生だと普通気づかないと思いますが、ここに気付くと先に進めます。
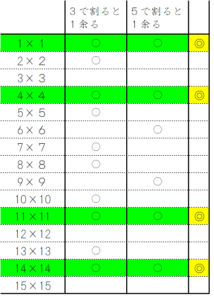
以下のような表を作って、3×5=15個の周期で考えます。両方の欄に〇がついた◎の部分が、「3で割っても5で割っても1余る数」です。
◎のついた部分は、先の「15で割ると1余る数」と同じ結果になりますので、以後は同じように解けばよいわけです。
この表を見ると、前述の「15で割った時の余り1の規則性」より、(周期が短い分)規則性がより見えやすくなりますね。
<解法3>因数分解を利用する方法
以下は私が最初に思いついた方法です。
中学数学の「因数分解」の公式を使うので、小学生向きでの解法ではないかもしれませんが、そもそも、問題自体が既に高校数学レベルなので、この解法で解いた小学生もいたのではないかと思います。
A×Aを式で表してみる
A×A(この後はA2と表記します)を15で割ると1あまるということは、A2÷15=□…1と表せるということです。よって、A2=15×□+1となります。ここまでは自然な考え方です。
ここで余りの「+1」が邪魔なんですね、せっかくA2とか、15×□と積の形になっているのに、「+1」が台無しにしています。
因数分解公式を使って式変形
そこで、邪魔な+1を左辺に移動します。すると、A2ー1=15×□となります。
単に1を移動しただけですが、移動する前の式と比べて劇的に扱いやすくなります。
なぜなら「左辺=A2ー12=(A+1)(Aー1)」と積の形で表せるからです。中学2~3年で習う因数分解の公式ですね。
よって、(A+1)(Aー1)=15×□となり、非常に扱いやすい式に変形できました。
後は、「場合分け」の世界
この後は場合分けです。式の形から、A+1またはAー1のいずれかが15の倍数になります。
(両方の数の差は2しか離れていないので、両方が15の倍数になる可能性はありませんね。)
「A+1」が15の倍数の場合、A=14,29,44,59,74,89の6通り
「A-1」が15の倍数の場合、A=16,31,46,61,76,91の6通り 合計 12通り
15=3×5を忘れずに
但し、答えはこの12通りだけではありません。右辺が15×□ ➡ 3×5×□とさらに素因数分解できるからです。
(A+1)×(Aー1)=3×5×□
3と5は「互いに素」なので、「A+1」が3の倍数ならば「Aー1」が5の倍数(あるいはその逆)というパターンになるわけです。
なお、「A+1」または「A-1」が、3と5の倍数(=15の倍数)であるケースはすでに検討済みであり、「A+1」と「Aー1」のいずれかが、3の倍数あるいは5の倍数でない場合、上記の式は成り立たないので、(以上の場合分けで)すべての場合を網羅できていることが分かります。
ちょっと工夫して
ということで、ここでまた「A+1」が3の倍数の場合…などと「場合分け」をしていっても良いのですが、少し面倒です。
左辺をよく見ると、(A+1)と(Aー1)となっていることから、2数の差が2であることが分かります(当然、(Aー1)<(A+1)です)。
例えば、5の倍数が「A+1」のとき、3の倍数は5の倍数より2だけ小さい数(Aー1)となり、5の倍数が「Aー1」のとき、3の倍数は5の倍数より2だけ大きい数(A+1)になります。
ということは、5の倍数を基準に±2した数が3の倍数になっていれば良いわけです。
15の倍数は先に調べているので、15の倍数以外の2桁の5の倍数を調べます。
この数を列挙すると、10,20,25,35,40,50,55,65,70,80,85,95の12個となります。
これら12個の数(3の倍数でない5の倍数)について、±2した数が3の倍数になるかどうかを調べれば良いのですが、調べると、12個のぞれぞれにつき対応する3の倍数が1つずつあることが分かります(例えば、20を例にとると、「ー2」の18が3の倍数になります)。

よって、答えは、15×□パターンの12通りと、3×5×□パターンの12通りの合計24通りとなります。
少し補足
なお、下の図の☆と★のどちらか一方が、必ず3の倍数になることは明らかなのです。
というのも、5nは3の倍数でない5の倍数と定義したからです。
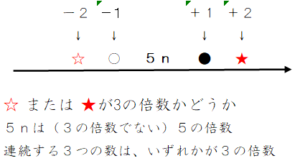
連続した3つの数があれば、その3つの中には必ず3の倍数が1つあります。
仮に☆が3の倍数でないとすると(連続する3つの整数は小さい順に)☆, 〇, 5n となりますが、この中で3の倍数は〇に決まります。しつこいようですが、5nを3の倍数でない5の倍数と定義しているので、5nは3の倍数になり得ないからです。
そして〇が3の倍数とすると、〇より3だけ大きい★が3の倍数になります。
逆に、☆が3の倍数であるとすると、☆より3だけ大きい●が3の倍数となります(この場合、★は3の倍数になりません。)
このように、3の倍数でない5の倍数を挟んで±2の数(☆と★)を考えた場合、どちらかが必ず3の倍数になる(両方とも3の倍数とか、両方とも3の倍数でないという場合はない)ことが分かります。
なので、10,20,25,…,95の個数(12個)がそのまま答え(の一部)になります。
終わりに
現実問題として、相当に学力が高い小学生のお子さんでない限り、この問題は解けないと思われます。
高校数学Aレベル、しかも教科書の章末問題とかのレベルは恐らく超えていて、高校数学でも応用レベルに属する問題だと思います。
なので、(灘中や一部の最難関中を志望するお子さん以外は)解ける・解けないにこだわる必要はないと思います。
むしろ、時間的余裕がある小6夏前頃までに、こうしたレベルの高い良質な問題を題材にして「整数の性質」を楽しんでみるといった姿勢が大事だろうと思います。
また、(これから高校数学を本格的に勉強し始める)中高一貫校の中3(中2?)あたりの生徒が、数学Aを学ぶ段階で取り組むのにちょうど良いと思います。
なお、数学Aで習う「合同式」を使うとA2≡1(mod15)より、A=1~15の中にA2≡1(mod15)となる数が4つあることがわかれば、10~99 ➡ 90個 90÷15=6周期より、4×6=24個と機械的に答えを出すこともできます(解いていてあまり面白味はないですが…)。
いずれにしても、灘中の入試問題は、高校数学を学ぶ前にもう一度見直してみるという使い方が良いのではないでしょうか。