マスター・オブ・整数(東京出版)より
今回も引き続き、高校数学レベルの整数問題をとりあげます。
ちなみに、マスター・オブ・整数(東京出版)のP11には次のような問題を含めて類題がいくつか掲載されています。
7で割ると1余り、9で割ると2余り、11で割ると3余る自然数のうち、1000に最も近いものを求めよ。(大学への数学 マスター・オブ・整数 P11より)
整数問題の難しさは「長大な約束事を理解しなければならない難しさ」(前掲書 P2)ではないので、小学生でも頑張れば取り組める問題も多くあります。また、数字の奥深さを知るには非常に良い題材だと思います。
私自身、「微積分」などの連続数学の分野については以前から仕事上の接点はあるものの、整数論をはじめとする「離散数学」の分野はあまり馴染みがないので、自分自身の勉強にもなります。
ちなみに今回取り上げる問題は、マスター・オブ・整数(東京出版)で紹介されている問題ではなく、以下に掲げる創作問題(類似問題)となります。
またここで紹介する解法についても、同書で紹介されている方法とは異なる点にご留意ください。
整数問題(割り算と余り)
3で割ると1余り、7で割ると5あまり、11で割ると3余る自然数のうち、1000に最も近い数はいくつですか。(創作問題)
中学入試でも良く出る「割り算と余り」の問題です。
数が2つではなく3つ出てくるのが少し厄介ですが、2つの数に分けて考えていけば恐れる必要はありません。
解答の手順
この種の問題は、以下の3つの手順で解くことで正解にたどり着きます。
なお、2段階と3段階は問題によってはほぼ同時に処理できたりするので、最大のポイントは第一段階となります。
第2段階: 最小公倍数で飛ばしていく。
第3段階:1000に一番近い数を注意深く調べる。
<第1段階>
3つの条件(3で割ると1余る、7で割ると5余る、11で割ると3余る)を満たす最小の数(=□)を見つけます。実はここが一番厄介な所です。基本的に書き出し作業となります。
<第2段階>
最小の数(=□)の次から、最小公倍数飛びに数を飛ばしていきます。この問題では、3つの数の最小公倍数が231(=3×7×11)なので、□から231飛びに数を飛ばしていきます。
最小の数:□ → □+(231×1) → □+(231×2) → □+(231×3)…
<第3段階>
□から231飛びで飛ばしていった数と1000を比較して1000に近い数を求めます。1000を挟んで「1000より小」、「1000より大」の2つの数が「候補」になるので、どちらの数が1000に近くいのかを注意深く比べます。
手順は以上です。
第1段階:最小の数を見つける
第1段階では条件を満たす最小の数を見つけることになります。
最小の数を見つけるには基本的に「書き出し」になります。
ただし、この問題のように3つの数(条件)が出てくるときは、少し工夫が必要です。
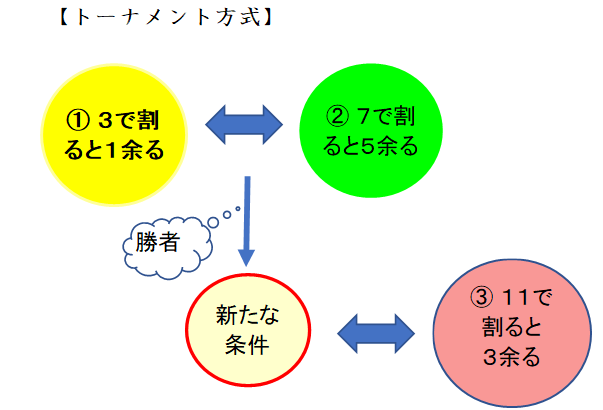
① 3で割ると1余る
② 7で割ると5余る
③ 11で割ると3余る
最初に、①と②の条件を満たす数を求めます(これを「①&②の条件を満たす数」とします。)
次に、「①&②の条件を満たす数」と③の条件を満たす数を求めます。
このように、3つの条件を同時に扱うのではなく、2つの条件に分けて段階を踏むことで、①~③の条件を満たす数が求まります。
まず①と②を戦わせてから、次に①&②と③と戦わせるので、「トーナメント方式」のイメージです。
それではやってみましょう。
最初に①と②の条件を満たす数を書き出していきます。
書き出す数は適当ですが、目安としてはだいたい小さい方の数(3で割ると1余る数)を10個くらい書き出せばよいと思います(もし10個で足りなければ順次追加します。)
素早く正確に書き出すことがポイントです。
3で割ると1余る → 1 4 7 10 13 16 19 22 25 28 …
7で割ると5余る → 5 12 19 26 33 40 47 …
上記の書き出して条件を満たす最小の数が19と求まりました。
19の次からは3と7の最小公倍数である21飛びに条件を満たす数が登場します。
つまり、 19+21=40,40+21=61,…となるので、19 40 61 82 …という数の並びとなります。
(①と②から得られた)新たな数の並びを①&②とします。
①&②は、「21で割ると19余る数」と言い換えられます(※)。
※ 数の並び(19 40 61 …)の方が意識できていれば、(問題を解く際には)特に言い換える必要はないでしょう。
よって、元の問題は次のような問題に置き換えられたことになります。
21で割ると19余り、11で割ると3余る数のうち、1000に最も近い数はいくつですか。
次に(トーナメントの勝者である)①&②と③を決勝で戦わせます。
ここも書き出しです。
①&② 21で割ると19余る 19 40 61 82 103 124 145 …
③ 11で割ると3余る 3 14 25 36 47 58 69 80 …
書き出していってもなかなか条件を満たす数が出てきません。
この種の問題の難しさは(決勝戦で戦わせるときに)、条件を満たす最小の数がなかなか現れないという点にあります。
解決策は一つ。「諦めずに根気よく書き出す」です。
①&② 21で割ると19余る 19 40 61 82 103 124 145
③ 11で割ると3余る 3 14 25 36 47 58 69 80 91 102 113 124
ようやく出ました! 124が(条件を満たす)最小の数です。そして、124の次からは231(=3×7×11)飛びに条件を満たす数が現れることが分かりました。
ここまで来れば8割方終了です。
第2段階:最小公倍数飛び
第1段階で「3つの条件を満たす数」は、「最小数が124、次からは231飛び」であることが分かりました。
言い換えると、初項:124、公差:231の等差数列となります。
つまりこの問題は、以下の問題に置き換えられたことになります。
初項が124、公差が231の等差数列で、1000に最も近い数を求めなさい
数学(算数)では、こうした「置き換え」や「言い換え」によって問題構造がシンプルになったり、見通しが良くなったりします。
小学生にはなかなか難しい注文ですが、中高生になったらこの点を意識することで数学の力は飛躍的に伸びると思います。
第3段階:注意深く調べる
本問の場合、たかだか「1000に近い数」なので、数列を意識しなくても、124 → 355 → 586 → 817 → 1048 …と最小公倍数で飛ばして調べていけば容易に答えが出るのですが、これが「10000に最も近い数」だったりすると、最小公倍数で飛ばしていくのは大変です。
そこで、もう少し一般的な解き方を考えます。
求める数をNとすると、N=124+231×★(★=0,1,2,3,…)と表すことができます。
そして、Nが1000に近くなるような★のあたりをつけるという方法をとります。
ここで、N=1000(※)と置くと、1000=124+231×★
⇒ ★=(1000ー124)÷231=3.7…
よって、★=3と4のときのNの値を調べれば良さそうだということが分かります。
※ あたりをつけることが目的なので、N=1000でも999でも構いません。別に商を正確に計算する必要はないので、小数点以下の結果などは不要です。
あるいは、1000ー124≒900とみて、「3 < 900÷231 < 4」などと頭の中で計算して、3と4に「あたり」をつけると計算が楽になります。
★=3のとき、124+231×3= 817
★=4のとき、124+231×4=1048
よって、1000に近いのは1048の方なので答えは1048となります。
補足:工夫も大切だが…
「3で割ると1余る」、「7で割る5余る」ような「ある数」を見つける際に、(書き出しではなく)、「ある数」に2を加えれば、「3でも7でも割り切れる」ことが分かります。つまり”「ある数」+2 ⇒ 21の倍数”ということになります。
よって、ある数(最小の数)=3×7ー2=19と求めることができます。これで少しだけ省力化できます。
この手の問題では、上記の3つのステップを踏めば解けるのですが、第1段階の「最小の数」を求める段階が力技になるケースが多いので、そこは少し時間と手間がかかります。
第一段階の時間短縮(手数削減)のため、「余りに注目して工夫」するといった視点も大切ですが、それ以上に(特に小学生の場合は)、素早く正確に書き出す訓練をする方が実践的と思います。
素早く正確に書きだすためには、言うまでもなく計算力(暗算力)が必要になります。