本日の記事はこちら ↓

長くなるので2回に分けます。
変わる算数・数学の学習過程
グルグルの図
――今年1月に行われた第2回大学入学共通テストの数学の問題を見ると、これから小、中、高での学びが変化していくことが如実に示されていたと思います。
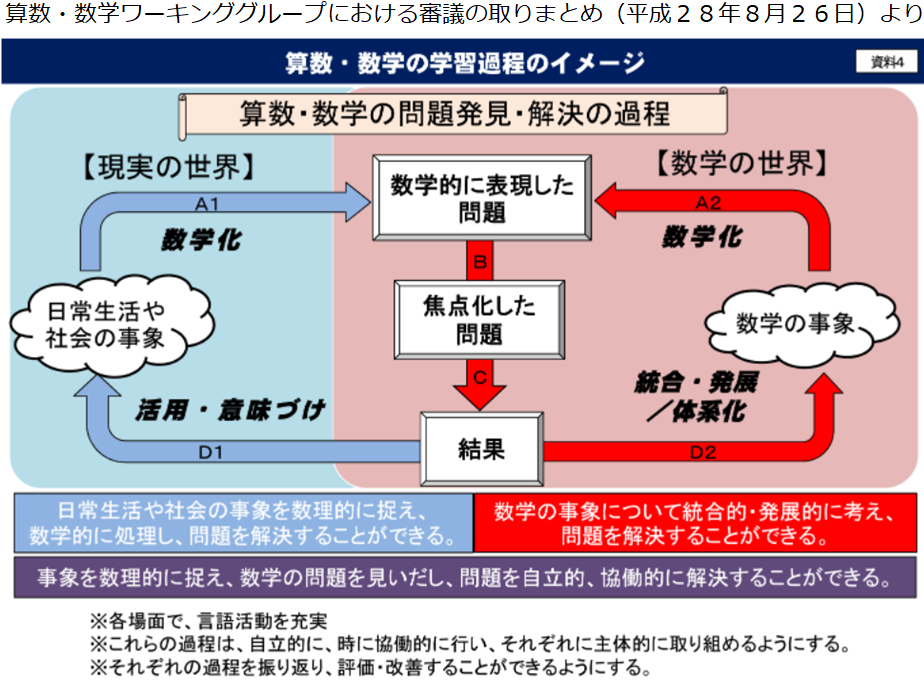
石田 (中略)その中で度々指摘してきたように、2回目となる今回の出題は、大学入試改革の検討過程で重ねて議論されてきた方向性がはっきり出たものだと考えられます。この方向性を示したものとして、教育関係者の間では「グルグルの図」と呼ばれている図1があります。ここには、今後の算数・数学の学習過程のイメージが示されています。
ここで示されているのは、「何のために数学を学ぶのか」という根源的な問いだと私は思っています。そのことが今回の共通テストでも問われたわけです。
「グルグルの図」というのがあることを初めて知りました。以下のような図ですね。
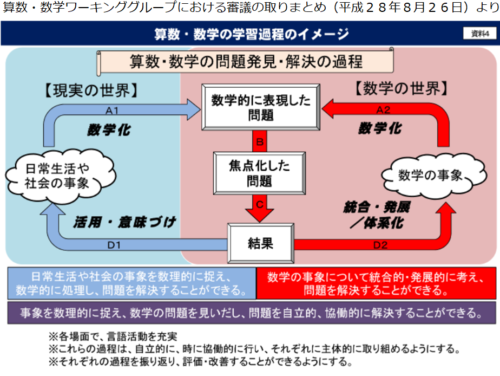
数学(算数)嫌いになる原因として、「『何のために数学を学ぶのか』ということがよくわからない」ということが指摘されます。
確かに、高校数学まで(小学校から通算すると10年以上)は、数学における基本的な約束事を延々と学ぶ段階なので、「数学が実際にどのように使われるのか」という点がなかなかイメージできません。
人間、意味の分からないことをやり続けるのは苦痛です。
実際、数学の実用性が垣間見える数学の応用分野(応用数学)は大学に入ってからの話なので、多くの学生がそこにたどり着くまでに力尽きてしまっても無理はありません。
そうした事情から、数学の脱落者をできる限り少なくしたいという思いが表れているのが「グルグルの図」ではないか、という印象を持ちました。
日本の数学教育の特徴(アメリカとの比較)
石田 これがグルグルの図と呼ばれているのは、図の中で数学的な活動が、左側でグルっと回り、右側でもグルッと回るからです。お子さんをお持ちの皆さんが普通に思い浮かべる「算数・数学の問題」というのは、図1の真ん中の部分です。「数学的に表現した問題」とは、教科書や問題集に載っている定型的な問題と考えてもらえばよいでしょう。
日本の数学(算数)教育が目指していたのは、「グルグルの図」の中央のルートをいかに効率よく学ぶかということだったと思います。
日本の教科書はアメリカの教科書などに比べると非常にコンパクトです。必要なエッセンスを盛り込み、冗長性(贅肉)をそぎ落とした形になっている。
一方で、実生活との関わりや実例(応用例)といった記述はかなり少なくなっていたり、説明に飛躍があったりするので、一度理解が追い付かなくなってしまうと、(教科書を使った)独習は難しくなる。
アメリカ(英語)の教科書はこの逆です。
教科書は大判でとにかく分厚い。高校数学あたりでも700ページ位の教科書は普通で、大学学部レベルの教科書だと普通に1000ページを超えてきます。しかも、B5版とかの大判なので、情報量的には日本の教科書の数倍はあるという印象です。
大学レベル教科書も高校数学の復習から入るので、ハードルが低い。しかも、同じ内容が手を変え品を変え様々な角度から説明されているので、説明の飛躍がなく、独習がしやすい。また、多色刷りで多くの実例が盛り込まれており、(私のような文系人間でも)読んでいて楽しい。
一方で洋書の教科書にはデメリットもあります。
(数学が)できる人から見ると、記述が冗長過ぎて、まとまりに欠けるという印象を受けるでしょう。
共通テストの冗長性
しかし、共通テストでは、この真ん中の流れに至る「前」の部分が問われているのです。図の左側「現実の世界」は、「日常生活や社会の事象」から数学的な事象を取り出すという観点からの問い掛けです。「数学の問題にたどり着くまでが長い」という感想が共通テストで出ているのは、この青い矢印(D1、A1)の部分が「長い」と言っているからですね。
先日、共通テストを自分自身で解いたときにも感じたのは、「問題文が長い」、「思考プロセスが長い」ということでした。
「数学的に表現された問題を効率良く解くこと」に慣れていると、今年の共通テストなどはかなり苦労すると思われます。
先の「日本の教科書」と「アメリカの教科書」にも通じる部分があります。
確かに、数学的活動の重要性や、(それを問う)今回の共通テストの趣旨はよくわかります。
しかし、比較的長い思考プロセスを辿らせるという方向転換をするのであれば、試験制度を含めて大幅な見直しが必要になると思うのです。
現行の試験時間は、いわば数学的に表現された問題を効率良く解くために設定された制限時間。長い思考プロセスを試すにはあまりにも短すぎる。
少なくとも現行の試験時間は見直す必要があると思います。
高度な中学入試に対応するために
以前、「難関中学の入試問題は究極の領域に」という記事の中で、受験算数が高校数学分野の先取りになっていることを書きました。
また、こちらの記事では、高校数学における「整数」や「場合の数」が(難関校の)入試問題で頻出領域になっていることを指摘しました。
まさに、今回取り上げた渋幕の問題などはその典型と言えるでしょう。実際、大学入試問題として出題されてもおかしくないほどレベルが高い問題です。
現在の(難関校の)中学受験は子供達にとって過酷な状況になっていると言えそうです。
中学受験のジレンマ
渋幕中の大問2(次回扱います。)を振り返ってみると、先の「グルグルの図」で言うところの、左側の事象(日常生活や社会の事象)だけに注目すればよいわけではありません。中央に位置するプロセス(=数学(算数)的な問題に置き換えて、解答を導くところ)まで要求されています。
つまり、具体的事象(=色の変化)を数学的問題(=場合の数)に落とし込まないと、制限時間内に解答することは難しい。
この点、思考プロセスがかなり長くなっているにもかかわらず、試験時間は長くなっていません。実は、共通テストと同様の問題が中学受験の方でいち早く発生しているのではないかと思うのです。
試験時間が変わらない中で、思考プロセスが長くなってしまった。
しかし、試験には合格する必要がある。
大手進学塾はこうした変化に対応するカリキュラムを設定する必要があるわけです。
そのためには、思考プロセスを速く回したり、ショート・カットしたりする必要がある。
つまり、さらなるパターン演習や大量問題演習を小学生に強いることになっている。
そうしないと、高い合格実績は出せませんので。
これが実情ではないでしょうか? ここに(中学受験の)大きなジレンマがあると思うのです。
高校数学Aの「数学と人間の活動」は要注目
難化する中学入試に対応するのは本当に大変なことですが、高校数学レベルの問題もかなり出題されている現実もあり、現実問題としてこうした潮流に対応せざるを得ないというのが実情でしょう。
2022年から新学習指導要領の下、数学Aでは「数学と人間の活動」という単元が新たに登場しました。
従来の学習指導要領では単独分野だった「整数」が(単独分野でなくなり)、「数学と人間の活動」のセクションに含まれるようになりました。また、身近な題材をテーマにした様々な題材が(多少、アドホック感はありますが)盛り込まれています。
中高一貫校の入試では、(良くも悪くも)高校数学(=大学受験)の先取り的要素を反映したものが扱われるケースがあるので、中学入試ではこのあたりの題材が今以上に扱われる可能性も高い。
したがって、受験生(小6生)をお持ちのご家庭は、高校数学Aの「数学と人間の活動」という単元には目を通しておいた方が良いと思います。
何も高価な(高校の)参考書を買う必要はなく、代表的な教科書出版会社の教科書で十分だと思います。
ちなみに、手元のある某出版社の改訂後の数学Aの教科書には、「数取りゲーム」、「ハノイの塔」、「日暦算」、「油分け算」、「ユークリッドの互除法」といった中学受験にも出題されている(されそうな)身近で興味深いテーマが掲載されています。
「問題を解こう」とすると親子ともストレスが増加しますが、遊びながら学ぶというスタンスで気軽に取り組めば、数学(算数)への興味も増すのではないでしょうか。
本日は以上となります。
次回は、渋幕2022年の入試問題(第2問)を取り上げたいと思います。