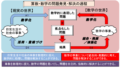
本日の記事はこちら ↓ 今回は後編です。

今年の中学入試問題より(渋幕中 2022年 大問2)
渋幕中の2022年 大問2(問題文)
渋幕中の2022年の大問2は以下のような問題です。
出題テーマは、難関校が好んで出題する「場合の数」で、大学受験に出題されてもおかしくないレベルだと思います。

前提知識は必要ないのか?
図2の渋谷教育学園幕張(渋幕)の今年の問題も同様のものでしたか。
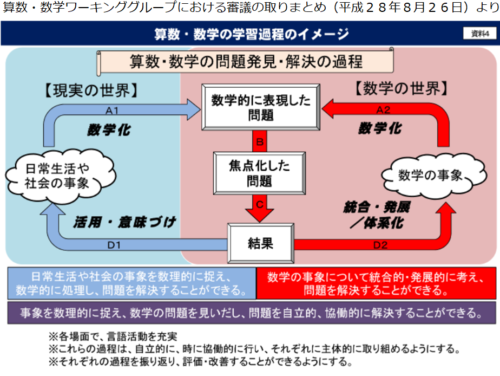
石田 この問題は、そもそもほとんど前提となる知識を要求していません。「○○算」といった解法や、計算技術に秀でていることは必要ありません。ただ、そこに書いてある文の意味を読み取り、それに従って作業できるか、つまり「読解力」が問われています。具体的な対象をよく観察し、そこに存在するルールを見つけ出して解決していくという点では、「グルグルの図」で問われている左側「現実の問題」のループに対応すると思われます。もちろん、そのまま「日常生活や社会の事象」ではありませんが、時間も前提となる知識も限られる中学入試では、このような出題になるのだと考えられます。
記事には、「ほとんど前提となる知識は要求されていない」とありますが、これは少し補足しないと誤解を生みそうですね。
「場合の数」の問題なので、「数え上げる」ことさえできれば誰にでも解ける。理屈上は確かにそうかもしれません。
しかし、正確に(漏れなく・重複なく)、かつ、効率よく数え上げるのはかなり難しい。
「知識がそれほど必要ない」というのは、高校数学の「微分・積分」、「指数・対数・三角関数」、といったかなり多くの約束事(前提知識)が前提となる領域に比べれば(前提知識)が少ないという意味に過ぎません。
しかし、この問題を解くのは(高校生ではなく)小学6年生。さらに言えば、試験なので制限時間内に解く必要がある。
中学受験勉強などほとんどしない普通の公立小学校に通う小学生が、試験当日に問題文を素直に読んで、その場で考えて解けるような問題ではありません。
グルグルの図(再び)
この問題を時間内に解くためには、「場合の数」の典型的な解法手法は最低限「知っている」必要がありますし、かつ、知っているだけでなく「使いこなせるように」しておく必要があります。
つまり、「グルグルの図」でいうところの、中央部分の「数学的に表現した問題」として解答する必要があるということです。
地頭の非常に良いお子さんは別かもしれませんが、凡人の私から見ると、こうした問題を小学生が時間内に解けるようになるためには、「いったいどれほどの訓練(勉強)が必要なのだろう」と畏怖の念すら覚えます。
小問1について
石田 (中略)この「言い換え」をする力は数学で非常に重要です。それは本質をつかみ出す能力だからです。「4色がすべて現れればよいのだから、4つの色の並べ方を数えればよい」と言い換えることができれば、4×3×2×1で求められると気づきます。計算は1行ですね。数え上げてもたいしたことはありません。
確かに、「4つのものを並べる順列」であることに気づけば、4P4=4×3×2×1=24通りと求まります。
公式を使うかどうかは別にしても、こうした「効率的な数え方(=解法)」を知識として知っているかどうかは重要だと思います。
記事にある通り、重要なのは「言い換え」の方です。
この言い換えができるかどうか、しかも、確信をもってそう言い切れるのかが難しい。
特に、些細な数え間違いが致命傷となる「場合の数」では、慎重にならざるを得ない。
もう少し慎重に考えると以下のようになるでしょうか。
(2)2番目の「青」は、「青」・「黄」・「緑」の3通りが考えられる。
(3)仮に2番目が「青」だとすると、3番目の「黄」は、「黄」・「緑」の2通りが考えられる。
(4)仮に3番目が「黄」とすると、左から順に「赤→青→黄」となる。
4色そろわないといけないので、右端は(緑に)自動的に決まる。
(2)~(4)を検討すると、3×2×1=6通り。(1)に戻ると、左端は「赤」の他、「青」・「黄」・「緑」が考えられるので4通り。6×4=24通りとなります。
これで本当に大丈夫でしょうか?
ためしに、左端を「赤→青」にすると、2番目の「青」は「赤」・「黄」・「緑」の3通り、2番目を「赤」とすると3番目の「黄」は、「黄」・「緑」、最後は…。ここまで確かめて、
そうか! 4つの色を順番に並べることと同じだから、結局、順列の問題だったわけか。
数学の苦手な私は上記のように慎重に考えます。 🙂
一方、樹形図を使って数え上げるとどうでしょうか。
これはやや時間がかかりますが、上手に数えれば、さほど時間をかけずに正確に数え上げることができます。
しかし、そもそも「樹形図」を用いた系統的な数え方(作法)を知らなければ話になりませんし、樹形図を描くにしても、それなりの習熟が必要です。
何の予備知識もなく、その場で解き方を考えて解けるような問題でないことは明らかです。
小問2について
石田 小問(2)では、2回スイッチを押した時、元の並びに戻るような規則の作り方が聞かれています。こういう時には、自分の手元で具体例を書いてみることが大切です。「赤、青、黄、緑」と書くのが大変な時は、順に「1、2、3、4」という数に対応させてしまうことができると作業は楽になります(これも問題の言い換え)。
1234→1243→1234のような例がすぐに作れるでしょう。これは「1→1、2→2、3→4、4→3」という規則ですね。ここから「2つの色は変えず、残りの2つを交換する」というルールが当てはまることが導けます。するとその数は、固定する2つの数の選び方(=入れ替える2つの数は自動的に決まる)を数えればよくなります。
そして、さらに「1→2、2→1、3→4、4→3」のように2つずつ入れ替えるケースもあることを忘れなければ、正解にたどり着けます。いわゆる「順列」の計算の仕方を知っていた方が効率はいいですが、数え上げてもそれほど手間はかかりません。
この問題は、3つのケースに「場合分け」する必要があります。
この「場合分け」という手法を(知識として)知っている必要があります。しかも、知っているだけでは不十分で、(しつこいですが)習熟して使いこなせるようになっていなければならない。
1番目のケースは、色が一切変わらないパターンです。これは以下のように1通りです。
① 左端 ☞(赤→赤→赤),(青→青→青),(黄→黄→黄),(緑→緑→緑)☚ 右端
2番目のケースは、「赤→青→赤」とか、「赤→黄→赤」というように、2度目に元の色に戻るパターンです。
ここで注意が必要です。「赤→( )→赤」の( )には3色(青・黄・緑)が入るから3通り、残りの「青→( )→青」・「黄→( )→黄」・「緑→( )→緑」の場合も同様に考えて、例えば、34=81通りなどとしてしまう危険性があります。
これは(よくありがちな)間違いです。このあたりが「場合の数」の厄介な所です。
実際に書き出してみると、以下の3通りしかありません。
②(赤→黄→赤),(青→緑→青),(黄→赤→黄),(緑→青→緑)
③(赤→緑→赤),(青→黄→青),(黄→青→黄),(緑→赤→緑)
この問題の背景には、赤(1つの色)の変化パターンが決まると、残りの色の変化パターンは自動的に決まるという重複順列の考え方があります。
具体的には、左端が「赤→(青)→赤」と決まった段階で、左から2番目の色は「青→(赤)→青」、さらに3番目は「黄→(緑)→黄」、そして右端は「緑→(黄)→緑」と自動的に決まってしまうのです。
結局、左端(の色の変化パターン)が決まれば、その他は自動的に決まるので、左端の「赤→( )→赤」の部分だけを考えれば良いということになります。
言われてみれば理解できますが、かなり高度で冷静な思考が要求されます。
やはり数多くの問題に触れ、何度も間違えながら(重複に注意するという)感覚を磨いていくしかないと思います。
しかも、ここで終わりではありません。
3番目のケースとして、「2つの色だけ変化して、2つの色はそのまま」というパターンがあるからです。
| 変化する色(2つ) | 変化しない色(2つ) |
| (赤→青→赤),(青→赤→青) | (黄→黄→黄),(緑→緑→緑) |
こちらは、「4色の中から変わらない2色を選ぶ」という「言い換え」で、組み合わせの問題として処理できます。4×3÷2=6通り(4C2)です。
結局、すべての場合をたし上げると、1+3+6=10通りとなります。
計算自体は簡単ですが、
① 場合分けを使って、3つの場合を漏れなく網羅する必要がある
② 重複に注意する
③「言い換え」をして「本質」に落とし込んでいく
といった高度な算数(数学)力が必要となります。
小問3について
石田 そうですね。最後の小問(3)は、3回続けて押した時に初めてすべてが赤になる規則についての問いです。これは(1)(2)よりも手間がかかりますが、実は右側の図が、この3回目が初めてすべて同じ色(この場合は青)になるケースになっています。ここを「読み取れる」かが大きなポイントでした。
――問題の中に書かれている図が実はヒントだった。これは経験しないとなかなか気がつかないかもしれません。
問題文中の図がヒントになっている(らしい)ことは、恐らく100%の受験生がわかると思います。
ただ、問題文に掲げられている例が、実は小問(1)や(2)のヒントではなく、小問(3)のヒントに直接関わっているというのは少し変化球だという気がします。
石田 与えられたものをしっかり受け止め、手を動かして試すことをいとわない。そういうことができる子を求めているのだと思います。さらに、この具体例を観察して(結果の観察)、「1回ごとに赤が1つ増えればよい」という本質を取り出す(抽象化・体系化)ができると、例えば「赤→赤、青→赤、黄→青、緑→黄」(先の数字での置き換えで言えば「1→1、2→1、3→2、4→3」。これで1=赤が1つずつ増えていく)のようなルールが、問われている条件を満たすことが分かるはずです。このような場合の数を求めて答えを出すことができます。
結論として、「3回押すとすべて赤になる」ということなので、例えば以下のようなパターンが考えられます。
(イ)「青→赤→…」(1回目で「赤」に変わるとその後何回押しても「赤」)
(ウ)「黄→青→赤→…」(2回目に「赤」に変わると、その後は「赤」)
(エ)「緑→黄→青→赤」(3回目に「赤」に変わる)
さらに、「(オ)赤から他の色を経由して赤に戻るケース」というのも考えられます。
しかしこの場合は書き出してみると、①「赤→青→赤→赤」、②「赤→青→黄→赤」のような色の変化になってしまうので、これはダメだと気付きます。
というのも、①では「黄」と「緑」、②では、「緑」の色の変化の規則が出てこないからです。なので、(オ)のケースは考える必要がない。
言い換えると、設問の条件に合致するためには、一度赤が出たら他の色に変わることはないという条件が必要だとわかります。結局、左端(赤)は、(3回押しても)「赤→赤→赤→赤」となり、色の変化パターンを考える必要がありません。
ここがこの問題の最も本質的な部分だと思います。
結果、(イ)~(エ)の色の変化パターンを考えればよいことになります。
(イ)は、「青→赤」の他に、「黄→赤」,「緑→赤」があるので全部で3通りです。
(ウ)は、「青→赤」の「青」の前の色を〇とすると、「〇→青→赤」の〇の場所に「黄」または「緑」が来る場合があるので、「黄→青→赤」,「緑→青→赤」の2通りがあります。
(エ)は、「☆→黄→青→赤」と続いた場合、残りは一色しかありません。(黄の前は)自動的に「緑」に決まるので1通りです。
結局、(イ)×(ウ)×(エ)で、3×2×1=6通りとなります。
正確に数えることの難しさ
一口に「数える」といっても、「自己流で数える」、「頑張って根気強く数える」というやり方では算数(数学)とは言えません。
「数える」にしても、正しい(ミスの出にくい)数え方のセオリー(定石)がある。それを知らなければ話にならないわけです。
また、間違いやすいパターンもいくつかあるので、それを認識しておくことで、ミスを未然に防ぐこともできます。
さらに、「場合分け」の手法、問題文から「規則性」を見抜いて「一般化」すること、そして、自分で実際に手を動かして調べてみるということも必要です。
こうしたものが幾重にも積み重なって、算数(数学)の基礎学力が構成されていると思います。しかも、教えられてすぐできるようになるわけではなく、根気強く勉強を続ける中で徐々に身についていくものです。
そのためにも、類題演習やパターン演習を相当にやりこまなければならない。
いずれにしても、こうした問題を解けるようになるには相当の準備が必要になるということだと思います。
正確に表現すると…
――確かに、事前に知識や手法を得ておくことより、「その場で読み取って考える」ことが求められていますね。
これも誤解を生みかねない表現ですね。
正確には、事前に知識や解法(樹形図、場合分け、基礎的な計算方法、重複への注意などを含む)を得て、典型的な「場合の数」の問題(=解法や考え方)に習熟しておくことに加えて、試験場で見慣れない問題が出題されても、今まで積み重ねてきた経験を駆使しながら、「その場で読み取って考える」ことが求められている、ということではないでしょうか。
こうした難しい問題が解けるようになるために、子供たちは日々相当に頑張っている(≒無理している)という事実について、大人達は認識する必要があります。
ゼロから100は生まれません。
初見の問題に対応するためには、その前提として、日々の学習(しかも相当に質の高い学習)の積み重ねが不可欠なはずです。