
管理人
こんにちは!
今日は、「予習シリーズ」の4年上の第7回の「分数の性質」をとりあげます。
来週から2週間春期講習に入るので、第7回は(2週間後の)4月5日の週となります。
今日は、「予習シリーズ」の4年上の第7回の「分数の性質」をとりあげます。
来週から2週間春期講習に入るので、第7回は(2週間後の)4月5日の週となります。

お母さん
いよいよ春休みですね。
そして休み明けは分数の回になるのですね。
そして休み明けは分数の回になるのですね。

管理人
はい。
2月に新4年生がスタートし、先週の第5回の組分けまでで1クール終わったわけですが、今週すぐに第6回がスタートですからね。
かなり大変だった思います。
ここでようやく一息つけるので、この間に消化不良部分を補っておきたいですね。消化不良となっていそうな重要テーマとしては、「線分図(和差)」、「計算のきまり」あたりが考えられます。
一方、春休みが終わると、第7回から第9回まで一気に進みますから、これまでの復習と同時に、第7回についても多少予習しておきたいところですね。
2月に新4年生がスタートし、先週の第5回の組分けまでで1クール終わったわけですが、今週すぐに第6回がスタートですからね。
かなり大変だった思います。
ここでようやく一息つけるので、この間に消化不良部分を補っておきたいですね。消化不良となっていそうな重要テーマとしては、「線分図(和差)」、「計算のきまり」あたりが考えられます。
一方、春休みが終わると、第7回から第9回まで一気に進みますから、これまでの復習と同時に、第7回についても多少予習しておきたいところですね。

お母さん
やることが盛りだくさんですが、「分数」についてはどのような点に注意して学習すればよいでしょうか?

管理人
まず、第7回で扱う分数の計算は「同分母の加減計算」なので、計算自体は楽です。唯一、以下のような減法については多少練習が必要でしょうか。
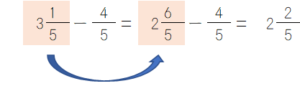

お母さん
いわゆる「借りてくる」計算ですね。

管理人
はい。
下巻で出てくる異分母の加減計算や乗除計算に比べると習熟に要する期間はかなり短くて済みます。また、帯分数で表される計算というのも基本的に小学校限定ですからね。
それでも、ある程度の慣れは必要ですね。
あとは、今週の小数の回で出てきた単位が分数でも扱われます。
距離の単位、重さの単位、容積(体積)の単位換算に加えて、第7回では時間の単位換算も出てくるのですね。
下巻で出てくる異分母の加減計算や乗除計算に比べると習熟に要する期間はかなり短くて済みます。また、帯分数で表される計算というのも基本的に小学校限定ですからね。
それでも、ある程度の慣れは必要ですね。
あとは、今週の小数の回で出てきた単位が分数でも扱われます。
距離の単位、重さの単位、容積(体積)の単位換算に加えて、第7回では時間の単位換算も出てくるのですね。

お母さん
単位については、春休み期間中に強化しておいた方が良さそうですね。

管理人
はい、おっしゃる通りです。
また、分数は小数よりもイメージしにくい数なので、春休みは分数の概念理解に取り組むのが良いと思います。
概念説明は塾では駆け足で進むので、自宅でじっくり、そして少し遊びも取り入れて学習するのが良いと思います。
例えば、「折り紙」を使うと分数の概念理解が進むと思います。
また、分数は小数よりもイメージしにくい数なので、春休みは分数の概念理解に取り組むのが良いと思います。
概念説明は塾では駆け足で進むので、自宅でじっくり、そして少し遊びも取り入れて学習するのが良いと思います。
例えば、「折り紙」を使うと分数の概念理解が進むと思います。


お母さん
なるほど。
折り紙全体を「1」として、折り紙の折り方や切り方で様々な分数を表せますね。これなら、3年生以下でも工作感覚で分数を楽しく勉強できそうです。
折り紙全体を「1」として、折り紙の折り方や切り方で様々な分数を表せますね。これなら、3年生以下でも工作感覚で分数を楽しく勉強できそうです。

管理人
そうですね。(新)3年生で整数計算が概ねできるようになっていれば、分数概念を遊び感覚で学ぶのも良いかもしれませんね。
また、切り方(折り方)を工夫すると、異分母の加減計算や分数の割り算などもこの折り紙で説明できるのですよ。
また、切り方(折り方)を工夫すると、異分母の加減計算や分数の割り算などもこの折り紙で説明できるのですよ。

お母さん
分数の割り算は、「分母・分子をひっくり返すもの」と習ったので、「そういうものだ」と思っていましたが、説明できるんですね。

管理人
はい。
ただ、「説明ができる」ということであって、別に「ひっくり返すものだ」と割り切って計算できれば良いのです。 😀
なお、単位換算については、今回は特に時間の換算が重要ですね。
以下のように、1時間=60分とか、1日=24時間といった換算を行いつつ、分数と絡めて計算できるようにすることですね。
ここでも折り紙が活躍します。
例えば「1時間の3分の2は何分か?」を計算する場合、1時間を60分に換算し、60分を3で割ってその2つ分だから40分と計算します。
今回、分数のかけ算は範囲ではないのですが、やっていることは分数のかけ算と同じですね。
今回は第1段の理解まで到達できればOKですが、いずれは第2段階の理解に到達します。
ただ、「説明ができる」ということであって、別に「ひっくり返すものだ」と割り切って計算できれば良いのです。 😀
なお、単位換算については、今回は特に時間の換算が重要ですね。
以下のように、1時間=60分とか、1日=24時間といった換算を行いつつ、分数と絡めて計算できるようにすることですね。
ここでも折り紙が活躍します。
例えば「1時間の3分の2は何分か?」を計算する場合、1時間を60分に換算し、60分を3で割ってその2つ分だから40分と計算します。
今回、分数のかけ算は範囲ではないのですが、やっていることは分数のかけ算と同じですね。
今回は第1段の理解まで到達できればOKですが、いずれは第2段階の理解に到達します。


お母さん
なるほど。
第2段階では、「60(分)×2/3=40(分)」と分数のかけ算になりますね。
第2段階では、「60(分)×2/3=40(分)」と分数のかけ算になりますね。

管理人
はい。
実はこの辺りの計算は、5年生で学ぶ「速さ」の単元においてスラスラできるようになっていることが前提なのですね。なので、今後長い付き合いになります。
なお、今回の応用問題では「全体の5分の2を使って、その残りの3分の1を使う…」といった「相当算」のような問題が出てきたりしますが、5年生になればできるようになるので、現段階ではあまり無理して理解する必要はないと思います。
実はこの辺りの計算は、5年生で学ぶ「速さ」の単元においてスラスラできるようになっていることが前提なのですね。なので、今後長い付き合いになります。
なお、今回の応用問題では「全体の5分の2を使って、その残りの3分の1を使う…」といった「相当算」のような問題が出てきたりしますが、5年生になればできるようになるので、現段階ではあまり無理して理解する必要はないと思います。

お母さん
なるほど。
第7回もなかなか盛りだくさんですね。
折角の春休みなので、楽しみながら概念理解に取り組むのが良さそうですね。
本日はありがとうございました。
第7回もなかなか盛りだくさんですね。
折角の春休みなので、楽しみながら概念理解に取り組むのが良さそうですね。
本日はありがとうございました。


