
前回の記事の続きです。問題を再掲します。
場合の数(ラ・サール中学 2019年)
①から⑦までの番号のついた座席が横1列に並んでいます。
① ② ③ ④ ⑤ ⑥ ⑦
人が座っている席のとなりには誰も座らないとします。
たとえば、①の席に人が座った場合②には誰も座らず、②の席に人が座った場合
①と③には誰も座りません。このとき、次の問に答えなさい。
(1)A、B、C、D4人の座り方は何通りですか。
(2)A、B2人の座り方は何通りですか。
(3)A、B、C3人の座り方は何通りですか。 (ラ・サール中学校 2019年度)
視点を変えて考える
今回は視点を変えて別解を考えます。
「視点を変える」と言っても、インスピレーションのように突然閃くわけではなく、過去に似たような問題をいくつか解いた経験を通じて「思い出す」という感じでしょうか。いわば経験値です。
難関校を目指してかなりパターン練習を積んでいる受験生の場合、以下のような方法のいくつかは「知っている」かもしれません。
椅子の間に「人」を入れる
高校数学の参考書では、比較的オーソドックスな解法として紹介されている方法です。
まずは(2)について考えます。
下の図のように椅子を5つ並べ、AさんとBさんを椅子の間に1人ずつ割り込ませることを考えます。AさんとBさんは下の図の6つの矢印のどこかに1人ずつ入ります。

AさんとBさんが下図の濃い色の矢印部分に入ったとして、実際の座り方は次のようになります。
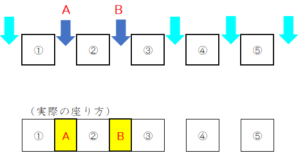
AさんとBさんがとなり合っていないことが分かります。
他にもいくつか選んで試してみると、AさんBさんがとなり合わないことが確認できます。
Aさん、Bさんが割り込むことができるのは全部で6カ所。
Aさんは6カ所どこでも割り込めるので6通り。Bさんは残り5カ所に割り込めるので5通りとなり、6×5=30通りとなります。
間に割り込むのが1人に限定されていることから、単純な順列問題に置き換えることができるので、計算は非常に簡単になります。
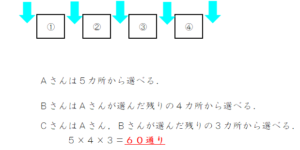
(3)についても同様の考え方で、まず椅子を4個置いて、その間にAさん,Bさん,Cさんを1人ずつ割り込ませます。
(2)と同様、各矢印には1人しか入らないので、結局、Aさんが選べるのは5カ所、Bさんが選べるのは4カ所、Cさんが選べるのは3カ所ということで、5×4×3=60通りとなります。
あるいは、5個の矢印から3つを選ぶ選び方(組合わせ)を計算して10通り、次にA,B,Cの3人の並べ替え(=6通り)を考えて、10×6=60通りと考えても構いません。
基本ユニットを作り、残りの椅子を入れる
間に入れていく方法としては、前述の方法がスマートですが、最初にとなり合わないような基本ユニットを作ってから残った椅子を間に入れていくという方法もあります。
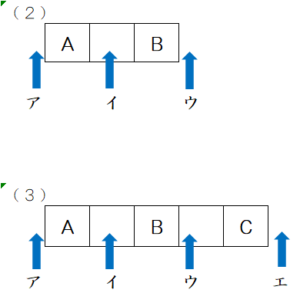
(2)であれば、「A□B」という(椅子3脚)ユニットを作って残り4脚の椅子を3箇所(ア,イ,ウ)に入れることを考えます。
一方、(3)であれば、「A□B□C」という(5脚)ユニットを作り、残り2脚の椅子を4箇所(ア,イ,ウ,エ)に入れていきます。
この方法のメリットは、「これならAさんBさん(Cさん)がとなり合わない全部の場合を網羅できていそうだな」という直感的イメージが湧きやすい点にあると思います。
ただ、先の解法のように「間に1人だけ割り込ませる ⇒ 単純な順列問題に帰着」という構造と違い、間に複数人が割り込む可能性があるので注意が必要です。
例えば、(2)であれば(ア,イ,ウ)=(4人,0人,0人)とか、(3)であれば、(ア,イ,ウ,エ)=(0人,0人,2人,0人)のように1箇所に複数人を割り込ませることができるので、「場合分け」が必要となります。
まず(2)ですが、「アが4人の場合、アが3人の場合…」と場合分けしていっても良いのですが、少し面倒です。そこで、(ア,イ,ウ)を各位の和が4になるような3ケタの数(但し0はどこにでも入る)と見立てて数字の組み合わせを考え、次に各位の並べ替えをする方法を考えます。
よくある「3の倍数の個数問題」と同じような解法です。
(ア,イ,ウ)に入る椅子の合計数は4脚なので、数の組み合わせは、(4,0,0),(3,1,0),(2,2,0),(2,1,1)の4パターンとなります。
この4パターンの並べ替えを考えると順に3通り、6通り、3通り、3通りとなり、合計で(3+6+3+3=)15通りとなります。
AとBの入れ替えを考えて「×2」をすると、15×2=30通りとなります。
(3)も同様に、各位の和が2となる4ケタの数(但し、0はどこにでも入る)と見立てます。
(ア,イ,ウ,エ)に入る椅子の合計は2脚で、組み合わせは、(2,0,0,0),(1,1,0,0)の2パターンとなります。
この2パターンの並べ替えを考えると順に4通り、6通りとなり、合計で(4+6=)10通りです。
A,B,Cの並び順の6通りを考慮して、10×6=60通りとなります。
自由に座らせ、後から椅子を入れる
あるいは、次のような方法も考えられます。
まず(2)ですが、1個だけ椅子を外しておいて、6脚の椅子にAさんとBさんに自由に座ってもらいます。
そして、AさんとBさんがとなり合ったら、2人の間に外しておいた椅子を入れます。
こうすれば、AさんBさんがとなり合うことはありません。
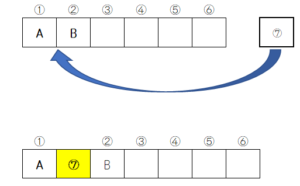
問題は、AさんとBさんが最初からとなり合わない座り方をしている場合に椅子をどこに入れるかです。
この場合は、AさんとBさんの間に椅子を入れるものとします。椅子を入れる箇所は、AさんとBさんの間であれば●のどこでも構いません。●に入れれば、AさんとBさんの間隔が椅子3脚分できる点で同じことになりますので。
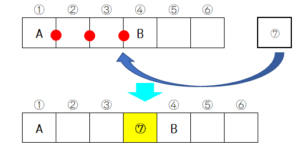
ところが、「Aさんの左」や「Bさんの右」に椅子を入れてしまうと、すべての場合を網羅することができなくなるので注意が必要です。例えば、AさんとBさんが①と⑦の両端に座るような場合を再現できません。
「AさんとBさんが6脚の椅子に自由に座る」➡「AさんとBさんの間に(自動的に)椅子を置く」という流れで考えることで、(2)の問題が、「AさんとBさんが6脚の椅子に座る問題に置き換わる」わけです。
これは、「4人を順番に並べる順列の場合、3人の並び順が決まれば残り1人の場所は自動的に決まる」という考え方を使っているわけです。
言われれば「当たり前のこと」ですが、慣れないとなかなか思いつかない発想だと思います。
また、この解法では椅子を入れる箇所にも制約が生じるので、小学生にはかなり難しいと思います。
いずれにせよ、このように考えることで、結局、AさんとBさんが6脚の椅子に座る座り方と同じことになります。答えは、6×5=30通りとなります。
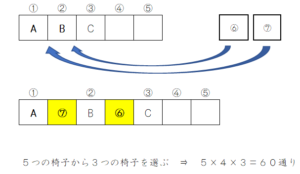
(3)も同様で、椅子を2脚外しておいて、Aさん,Bさん,Cさんの間に1脚ずつ入れていきます。
最初からとなり合っていない場合も、AさんとBさんの間に1脚、BさんとCさんの間に1脚入れるという方向で考えます。
そうすると、5脚の椅子に3人が座る座り方と同じになるので、5×4×3=60通りとなります。
理想と現実
上記の他にも別解はあるとは思いますが、数学の最も有効な勉強方法は「別解を考える」ことにあると思います
解法には、「筋の良い解法」や「そうでもない解法」など様々あるわけですが、良い解法や悪い解法、あるいは途中で行き詰ってしまった解法なども含めて、一つの問題を様々な角度から考えて、別解をいくつも考えることによって真の数学の力が身につくと思うのです。
こうした学習効果の高い問題を半日ぐらいかけて塾生と講師が議論をしながら理解を深めていくのが理想的だと思うのですが、現実には「中学入試」というイベントが控えているので、そんな贅沢な時間はとれそうになりません。
中学受験の現実
現在の中学受験の勉強では、塾から課される大量の課題を流れ作業の如くこなしていかないと、未消化の課題がドンドン累積していきます。到底、1つの問題に対していくつも別解を考えるような時間的余裕はありません。
したがって、最短距離で解ける解法を覚え、それを反復問題演習を通じて効率的にマスターしていく流れになります。
仮に高校数学レベルの問題が入試問題で出題されても、大手受験塾ですぐにパターン化して生徒に教え込み、(難関校を狙う)生徒は問題演習を繰り返すことで解けるようになってしまいます。
もちろん、「解法パターン学習」も必要ではありますが、行き過ぎると「単に答えが短時間で出せればそれでOK」みたいな味気ない勉強になってしまいます。
例えば、先の解法では「A,Bがとなり合わない」という条件を「椅子と椅子の間(矢印部分)にA,Bを入れていく」という条件に置き換えています。
この辺りが非常に面白い発想なのですが、矢印の所にAさんとBさんを入れていくとして、「本当にこれでとなり合わないすべての場合が網羅できているのだろうか」ということに疑問が湧くと思うのです(少なくとも、私はそうした疑問が湧きました)。
そこで、自分で図を描いてみたり色々試したりしてみた結果、ようやく合点がいくと思うのです。
しかし、(時間に追われる中で)こうしたことを行わずに、単に「こういう問題の場合は、間に入れていけばいいんだ」というように解法の暗記になってしまうと、少し捻られると手も足も出なくなってしまうように思います。
それ以前に、「あまり面白くない勉強」になってしまうと思うのです。
「いたちごっこ」は続く
中学入試でどのような問題を出題しても、必ず解答があり、試験時間内に解ける解き方があります。
結局は(中学校がどのような問題を出そうとも)受験塾が対策を行って(パターン化して)解けるようにしてしまうといういたちごっこは今後も続くことでしょう。
この結果、受験生がこなす学習量は毎年増加の一途をたどります。その負担は、受験生である小学生とその親御さんに確実に降りかかっているわけです。
量がどんどん増えていくと(時間は有限なので)、どこかで辻褄を合わせるしかありません。
辻褄合わせとして、「短時間で効率的にこなす」方にどうしても意識が向いてしまい、表面的な理解になってしまう危険性があります。
じっくり腰を落ち着けて勉強するのは、中学(高校)に入ってからということになるのでしょうか。


