受験に「タラレバ」は禁物ですが、「こんな算数の教え方をすると力がつきそう…」と感じたことを書き留めたいと思います。
典型題(一行題)は最短距離で
入試問題の中の「典型題」あるいは「一行題」と言われるものがあります。
例えば、以下のような問題です。
7で割ると2余る2けたの整数はいくつありますか。
最近の難関校の入試では、この種の典型題(一行題)はあまり出なくなっていますが、① 解き方を知らないと解けない問題があること、② 入試に良く出る総合問題は一行題が組み合わされているものが散見されることなどから、是非ともマスターしておきたい問題です。
一行題は、「最短距離で解ける解法を理解し、短時間で確実に解けるようにする」ことがポイントになります。
典型題(一行題)は論点がすっきりしている(考え込むような問題ではない)ので、勉強しやすいのですが、意外に手こずるケースもあるようです。
その原因がどこにあるのか、少し考察してみました。
典型題を解く準備
手許にある5年生の予習シリーズには、以下のような「例題」があります。
2けた(10~99)の整数について、7の倍数は何個ありますか。
(予習シリーズ5年上 第1回 倍数と約数 必修例題1)
大人の目から見ると、この例題と上で挙げた典型題はまったく同じ構造の問題で、例題が解ければ典型題も解けるはずです。
ところが、小学生の子供にとっては必ずしもそうではない。「あまり」があるかないかで、全然別の問題に見えてしまうこともあるわけです。
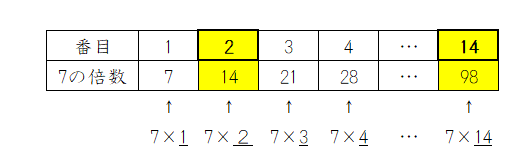
恐らく、上記の典型題と例題の関連性をスムーズに理解できるお子さんは、以下のような(7の倍数が2ずつ平行にズレていく)数直線のイメージが頭の中にあると思うのです。

このイメージがあれば、「ズレの部分だけ修正すれば、あとは7の倍数と同じ考え方をすればよい」と分かるので、仮に初期段階では典型題が解けなくても、講師の説明や解説を読めばすぐに理解でき、短期間で定着すると思われます。
果たして例題の理解は大丈夫か?
典型題がスムーズに解けないケースとして、例題レベルの理解があやふやになっているケースもあると思います。
上記の例題の説明は以下のようになっています。
99÷7=14あまり1より、2けたの7の倍数は、7×2,7×3,…,7×14 → 14-1=13個
(予習シリーズ5年上第1回 約数と倍数 必修例題1)
極めて簡潔で正しい解説なのですが、簡潔が故に誤解を生じやすい書き方になっています。
特に、お子さんに教材を与えて勉強させているだけだと、とんでもない誤解をする危険性があります。
例えば、「14-1=13」の部分。
これは、1~99までに7の倍数が14個あり、1~9までに7の倍数が1個あることから、「14-1=13」となっているわけです。
ところが、直前の計算結果には「14あまり1」というのがあるので、(自宅学習で子供に任せてしまうと)「よく分からないけど、とりあえず商(14)からあまり(1)を引けば答えが出るのだ」などと、誤解してしまう危険性があります。
こうした誤解は、塾などで講師の説明をよく聞いて学習していれば生じないのですが、塾の授業がよく分からないまま復習したり、あるいは、自学自習で勉強を進めている場合は注意する必要があると思います。
例題の初歩的な解き方
上記の5年生の例題ですが、このような単純な問題でも解き方はいくつかあります。
まず出発点として、「7の倍数だから7の段を考える」という発想が生まれます。
とりあえず、7×1=7,7×2=14…と書き出していって、7×14=98,7×15=105まで来たとき、「105はダメだから、98までだな」と気が付けば、書き出し&数え上げで正解の13個に到達します。
「書き出し&数え上げ」はprimitiveな解法ではありますが、題意自体はしっかりつかんでいるので、(無理に式で解かなくても)小5初期においては及第点だと思います。
集合として考える
例題レベルの問題であれば、「書き出し&数え上げ」だけで(13個という)正解に到達できます。
しかし、「3けたの7の倍数の個数」を求めるような場合には、書き出して数え上げていては時間がかかり過ぎるし、間違いやすくなります。
そこで、次のステップとして、7×1=7,7×2=14,…,7×14=98の1,2,…,14が何を意味しているのかを考えさせます。
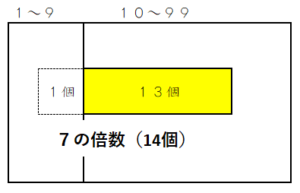
一つの方向性として、「1~99までに7の倍数が14個ある」ということを認識させることが考えられます。これは、集合的な考え方と言えるでしょう。
そうすると、1~99までに含まれる7の倍数(14個)から、1~9に含まれる7の倍数(1個)を除くという考え方により、14ー1=13個と答えが出ます。
数列的に考える
一方、7×14=98から、98は14番目の7の倍数であることを認識させます。
こちらは数列的な考え方と言えるでしょうか。
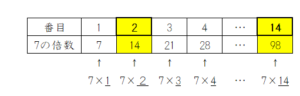
(条件を満たす)14番目の数(最大の数)と2番目の数(最小の数)を求めれば、14-2+1で(条件を満たす数の)個数が出るという考え方です。
考え方の差によって、「14ー1=13」となるか、「14-2+1=13」となるか、微妙な違いが出てくると思います。
集合的に考えるか、数列的に考えるか
「集合的に捉えるか」、「数列的にとらえるか」については、どちらでも良いと思いますが、どちらかの方法で説明すると決めたら、整合的な説明をすることが大切だと思います。
「集合の思考」がしっくりくる子供には、(数列的な)「14ー2+1=13」という式の意味はピンとこないでしょうし、逆に数列(〇番目)で考える子供には、「+1はしなくて良いの?」という疑問が生じるかもしれません。
計算で効率的に求める
最後に出てくるのが、「99÷7=14あまり1」という式です。
この式には以下の2つの意味があり、「集合を意識させるか」、「数列を意識させるか」によって、式の意味の説明の仕方も若干変わってくるかもしれません。
| ☒ 1~99までに7の倍数が14個ある → 集合 ☒ 1~99までの最大の7の倍数は14番目の数である → 数列 |
この式は大人には分かり易いのですが、子供にとっては案外分かりにくい気がします。
しかも、例題レベルの問題であれば、書き出した方が早くて簡単なので、お子さんは大抵書き出しスタイルを好むので、なかなか式を書きません。親御さんから「式を書くように」と言われて、親子バトルが発生し始めるのもこの頃からでしょうか?
最初から式の意味をしっかり理解できて、(予習シリーズのような)解答で解けるお子さんは別にして、式に拒否反応があるのならば、教える時期を先延ばしにした方が良いかもしれません。
初期段階では(子供には)計算の有難みは分かりませんが、いずれ書き出し個数が増えてくる問題が出てくると、計算による解法が必要となります。その頃になると、数の感覚も大分身についてくるので、式への拒否反応も薄れてきます。その段階まで待ってみるのも一法かもしれません。
こんな感じで、お子さんのレベルに合った教え方をしたり、時期が来るまで見送ったりするような段階的な教え方ができれば、算数嫌いにならずに学力を高めることができるのでは…などと思いました。