前回の記事に続き日暦算です。
準備作業が済んだので、いよいよ本題に入ります。
日暦算に挑戦
(2)ある年の12月25日は土曜日です。同じ年の7月30日は何曜日ですか。
(1)は前に進む問題、(2)は後ろから戻る問題です。
(2)の方を苦手にするお子さんが多いように思いますが、基本的に解き方は同じです。
日数の計算
標準的な解き方では、7月30日から12月25日までの日数に注目します。
ここでの重要ポイントは、7月30日を含めるか否かという点です。
テキストの解説などを見ると含めるケースが多い(=期間の計算をする)ようなので、ここでも7月30日を含めて計算します。
まず、7月30日~12月25日までに何日間あるかを計算します。
単純な計算ですが、(加える月が増えると)計算ミスが出やすくなるので、以下のように対応する月を書き添えることで、計算ミスを防げますし、検算もしやすくなります。

ここまでが第一段階です。
② 日数のたし算は計算ミスしやすいので、ミスを防ぐ&発見する工夫をする
日数÷7=○あまり□
さて、次は上記で求めた日数(149日)を7(日)で割る段階です。
149(日)÷7(日)=21 あまり2(日)
商の21が目に入りますが、求めたいのは曜日なので「あまり2」の方に注目します。「あまり=曜日」の対応関係の意識を持つことが大切です。
お子さんが、「149÷7=21あまり2」という式を見て、「21週間と少しあって、「あまり2」が曜日に対応しているんだろうな」ということが理解できれば基本構造が理解できているので大丈夫です。
では、「あまり2」は正確に何曜日に対応しているのでしょうか。ここで、曜日の分かっている7月30日に着目し、あまりを求めます。
| 日付 | 7月30日 | 12月25日 | 曜日の分かっている 7月30日を基準に! |
| あまり | ? | 2 | |
| 曜日 | 金曜日 | ?(求めたい曜日) |
7月30日(金)を1日目と考えると、1÷7=0あまり1で、あまり1が金曜日に対応しているとわかります。
「1÷7=0あまり1」は計算するまでもないのですが、「あまりと曜日が対応する」というのが日暦算の最大のポイントなので、一回はしっかりと認識しておくべきと思います。ここが曖昧だと、「1日ズレていた」というもったいないミスが頻発します。
| 日付 | 7月30日(基準) | 12月25日 | あまり1⇔金 あまり2⇔? |
| あまり | 1 | 2 | |
| 曜日 | 金曜日 | ?(求めたい曜日) |
あまりと曜日の対応関係が決まれば、2日目(7月31日)は2÷7=0あまり2で、あまり2が土曜日と分かります。3日目以降は同じように考えていくだけです。
この問題であれば(149÷7=21あまり2なので)、12月25日は土曜日とすぐに分かります。
ただ、せっかくなので、あまりと曜日を次々に対応させて、以下のような表を作ると良いでしょう。慣れればあっという間に作れるようになりますし、この表が出来上がれば、日暦算は解けたも同然です。
| あまり | 0 | 1(基準) | 2 | 3 | 4 | 5 | 6 |
| 曜日 | 木 | 金(基準) | 土 | 日 | 月 | 火 | 水 |
② 曜日の分かっている日(7月30日)のあまり(=1)と曜日(=金)を対応させ、あまりと曜日の関係を決める。
③ あまりと曜日の対応表を作り、曜日の分からない日(=12月25日)のあまり(=2)から曜日(=土)を見つける。
先の日付から戻る問題
例題2の(2)も、149÷7=21あまり2 を計算するところは同じです。
ただ、(2)では、先の日付である12月25日(土)があまり2に対応するので、「あまり2=土曜日」が基準日となります。
初日の7月30日は含めるので、必ず、1÷7=0あまり1という式になり、あまり1を曜日に対応させることになります。
「あまりと曜日の対応表」(省略します)を作れば、あまり1(7月30日)は金曜日と分かります。
| 日付 | 7月30日 | 12月25日(基準) | あまり2⇔土 あまり1⇔? |
| あまり | 1 | 2 | |
| 曜日 | ?(求めたい曜日) | 土曜日 |
補足1:7月30日を含めない方法
日暦算に出てくる「7月30日を含めて○日間」というのは、普段あまり馴染みがない概念です。
例えば、「8月1日(今日)の1週間後は8月8日である。」といった表現は良く使いますが、「8月1日から8月8日まで8日間ある」といったことはあまり意識しませんし、こうした言い回しも、日常生活ではそれほど出てこないと思います。
そこで、慣れ親しんだ(初日である7月30日を含めずに)上記の問題を解くと、「7月30日の148日後が12月25日になり、148÷7=21…1となります。
「あまりと曜日の対応」を考える際に7月30日(金)が基準になることには変わりはありませんが、今度は7月30日を日数に含めていないので「0日」。「あまり0」となります。
ここさえ注意すれば、「あまり0(7で割り切れる)=金曜日」を基準にして、12月25日はあまり1なので、あまり1=土曜日となります。
恐らく、7月30日を含める解法が主流と思われますが、通っている塾の教え方や使っているテキストの解説が「初日を含む」 or 「含まない」のどちらの考えになっているかは確認した方が良いと思います。
補足2:おばけカレンダー
「日暦算」で、「おばけカレンダー」というのを使う方法もあります。
これは、12月25日を7月○日という形にして、(早い方の月の)7月のカレンダーの中に組み込んでしまうというやり方です。実際にはないカレンダーなので、「おばけカレンダー」と呼ぶようです。
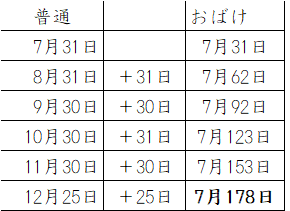
この方法で(1)の問題を解くと、12月25日 ⇒ 7月178日になり、178÷7=25あまり3となります。よって、あまり3を曜日と対応させることになります。
ここで、7月30日の曜日が金曜日で、30÷7=4あまり2なので、あまり2が金曜日に対応します。あまり3=土 → あまり4=日 …となるので、以下のような表が完成します。
| あまり | 0 | 1 | 2(基準) | 3 | 4 | 5 | 6 |
| 曜日 | 水 | 木 | 金(基準) | 土 | 日 | 月 | 火 |
先述の通り、12月25日は「あまり3」に対応する曜日なので、土曜日とが分かります。
(2)の問題のように、12月25日が土曜日と分かっている場合、(12月25日の)「あまり3=土曜日」を基準に、(7月30日の)「あまり2」が何曜日かを調べればよいわけです。
曜日の分かっている方の「あまり⇔曜日」セットから、曜日の分かっていない方の「あまり⇔曜日」セットを求めるという基本的流れは一緒です。
「おばけカレンダー」を用いる方法を使うと、「+1をするかどうか」などということは考えずに、「あまりと曜日の対応」だけに着目すれば解けます。
途中で何をやっているのか分からなくなってしまうお子さんには有効な方法ではないかと思います。
期間の起算日は結構やっかいな問題
初日を入れたり、あるいは、入れなかったりすることの紛らわしさは、「日暦算」だけでなく、法律関係などにも現れます。ちなみに、民法では以下の通り、初日不算入が原則です。
民法第140条(暦法的計算による期間の起算日)
日、週、月又は年によって期間を定めたときは、期間の初日は、算入しない。ただし、その期間が午前零時から始まるときは、この限りでない。
一方、原則があれば例外もあるわけで、同じ民法には次のような規定があり、こちらは初日算入となります。
-
民法第143条(暦による期間の計算)
1.週、月又は年によって期間を定めたときは、その期間は、暦に従って計算する。
2.週、月又は年の初めから期間を起算しないときは、その期間は、最後の週、月又は年においてその起算日に応当する日の前日に満了する。ただし、月又は年によって期間を定めた場合において、最後の月に応当する日がないときは、その月の末日に満了する。
(例外規程である)初日不算入の最も身近な例は「年齢」。
明治35年の「年齢に関する法律」で、誕生日の前日に1つ歳をとるということが定められています。
明治三十五年法律第五十号(年齢計算ニ関スル法律)① 年齢ハ出生ノ日ヨリ之ヲ起算ス② 民法第百四十三条ノ規定ハ年齢ノ計算ニ之ヲ準用ス
<学校教育法>
第二十二条 保護者(子女に対して親権を行う者、親権を行う者のないときは、後見人又は後見人の職務を行う者をいう。以下同じ。)は、子女の満六才に達した日の翌日以後における最初の学年の初から、満十二才に達した日の属する学年の終りまで、これを小学校又は盲学校、聾学校若しくは養護学校に就学させる義務を負う。<学校教育法施行規則>
第五十九条 小学校の学年は、四月一日に始まり、翌年三月三十一日に終わる。
上記の法律の規定を組み合わせると、例えば、2015年4月1日生のお子さんは、2021年3月31日に(法律上)満6歳になるので、学校教育法と同施行規則により、2021年4月1日から小学1年生になるわけです。
前年の4月2日~当年の4月1日まで同じ学年になるので、少し違和感を覚えるのではないでしょうか。
いずれにしても、年、月、日…といった期間にアンテナを立てる(=意味を注意深く考える)ということが、日暦算に強くなる秘訣かもしれません。

