(前回から間が空いてしまいましたが)本日の記事はこちら ↓

今回は続編として駒場東邦中学の2022年の算数の入試問題を取り上げたいと思います。
駒場東邦中学2022年大問3(超難問)

過程をしっかりたどる力
石田 今年の駒場東邦の問題は、どれも本格的で非常に難問ぞろいでした。
(中略)
まずは、問題文の提示している状況の理解ができるかどうかが初めの壁になります。
2022年の駒場東邦の算数の問題は非常に難しかったようです。
駒場東邦中学の入試統計資料を見ると、算数の平均点は、受験者平均で29.6点、合格者平均で35.5点(100点満点換算 ※)ということなので、今回の大問3についても、小問1あたりができていれば、御の字だったのではないでしょうか。
※ 算数は120点満点のため、100点満点に換算して表記
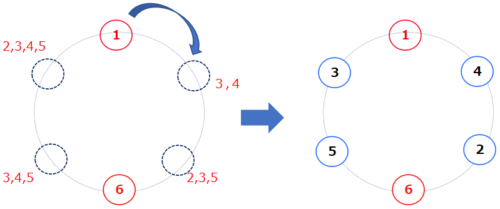
石田 そして「1からAまでの整数」が並べられ、このルールにしたがって1から出発した時に、「2からAまでのすべての整数にちょうど一度ずつ到達することができる」ようにする、というのが条件です。小問(1)ではA=6の時、つまり1から6までの整数を円形に並べた時に条件を満たす並び方が聞かれています。
――これをやみくもに並べて解くのは大変そうです。
石田 はい。実は先ほどの渋幕の問題と同じように、問題文の中に重要なヒントが与えられています。でも、あまり明示的でないので、これに気が付く受験生が少なかったかもしれません。(1)ではまず、「最後に到達する整数はいくつですか」が聞かれ、次に「このとき1の真向かいに並んでいる整数はいくつですか」が聞かれています。
確かに問題文中にヒントがありますが、気づきにくいです。
むしろ解いている過程で気づくという感じでしょうか。
いくつか試してみて”6”を置いたとき、「あれ? 6を置くと1周して元の場所に戻っちゃうな」ということに気づくかどうか。
ここから、「6を置くのは最後でなければならない」という発想に結びつけられるかどうか。
このあたりが思考の出発点になるように思います。
石田 どうしても受験の算数では、答えを出す事が最優先となってしまい、答えが合っていればいい、となりがちです。これは、中学以降の数学を教える先生方が最も嫌う態度の一つです。数学は、結果よりも過程が大切だからです。
これは東大がホームページ上で公開しているアドミッションポリシーの中で、高校生に求める数学の中身としても言及されています。数学で要求されるような「過程をしっかりたどる力」が、今後の学問や仕事で求められる力につながるのです。そういうことを出題者側は考えていると思います。
――それが数学を学ぶことの大切さ、ということなのですね。
これは正論です。
しかし、敢えて言うならば、入学試験の制限時間はかなりタイト。
限られた試験時間の中で、試行錯誤しながら過程をしっかりたどるというのは(理想論ではありますが)、現実問題としては限界があると思います。
その難しさは、(先述の)平均点の低さにも表れているわけです。
本来であれば、教室で1時間とか2時間かけて(あれこれ議論しながら)じっくり学ぶのに値する問題も、入学試験という(限られた時間で1点でも多く得点するという)局面においては、単なる「捨て問」になってしまいかねません。
制限時間のある入試において、いかに「考える力」を問うのか。
なかなか難しいテーマだと思います。
小問(1)について
石田 (中略) 6という数に途中で到達したら、6進むことになります。ところが、円形に数は並んでいるので、6進むと6に戻ってしまいます。「すべての整数にちょうど1回ずつ到達する」のですから、途中に6は存在できません。ですから,最後の数は6でなければいけません。
そうすると、次の「1の向かい側の整数」は何でしょうか? ここは少し難しいですね。全体の合計に着目する、ことに気付くには少し経験が必要かもしれません。最後の数は6であることが分かりました。この6を除くと、1からの移動量の合計は1+2+3+4+5=15となります。1周は6ですから、15ですと2周回ってさらに3進むことになります。
これはちょうど1の向かい側ですね。ですから、1の向かい側は6になるわけです。後は残りの「2、3、4、5」を4つの場所に当てはめていくことになります。ここはルールに沿うように、試行錯誤しながら順番に数を当てはめていくことになります。
「6を置くのが最後」と分かったとしても、その先の展開も難しい。
⇩
✅ 2~5を置く順番は不明だ。
⇩
✅ (2~5を)置く順番はともかく、6以外の数を置き終わった状態を考える。
⇩
✅ 仮に「6」が下図の●の位置だったとする(仮置き)。
⇩
✅6を置く前に(合計で)、1+2+3+4+5=15だけ進むから、
15進んだ位置が●に対応するはずだ。
⇩
✅ 15÷6=2あまり3だから、(1から)2周回ってさらに3だけ進む位置が●になる。
-500x245.png)
上記のように考えると、1の真向かいに6が来ることがわかります。
配置は試行錯誤で
この後で、具体的な配置を考える必要がありますが、これは試行錯誤になるでしょうか。
ただ、やみくもに数値を当てはめるのではなく、条件を絞っていくことで、効率的な当てはめができると思います。
例えば、1からスタートして、次の場所に入る数は3,4のいずれかなので、ここを手掛かりにトライすると、試行錯誤の回数が減り、解答が素早く導けると思います。
小問(2)について
石田 次の小問(2)では、A=7の時は条件を満たすようには並べられないことの説明が求められます。このような「説明」は、中学以降の数学では「証明」として求められる作業です。先ほど述べたように、数学では結果が言えるだけでなく、その「途中」が「つなげられるか」が重要です。そういった姿勢を持っているかを聞いているのでしょう。
ここでもやはり、小問(1)の結果を振り返って、そこから本質をつかみ出して活用できるかがポイントです。先ほどの作業の結果から、この場合も最後の数はA=7になりますね。そして、先ほどと同じくすべての移動量の和を求めると、今回は1+2+3+4+5+6=21になります。21は7の倍数ですから、21進んだら初めの1の場所に戻ってしまうことになります。これでは最後の7を置くことができませんね。これで説明ができたことになるわけです。
この問題も非常にレベルが高い問題です。
A=7における円周上の点と7でわった時のあまりを対応させれば分かりますが、1~6まで置いたとき、1~6までの数の和(1+2+3+4+5+6)が21になるので、21÷7=3となります。
7でわった時にあまり0となる位置には「1」があるので、「1」と重なってしまいます。
つまり、A=7の場合は7を置く前にゲーム終了ということになります。
うまく説明するのは難しいですが、背理法的に説明すると以下のような流れになるでしょうか。
① 1~7を置くことができるとして、1~7の数を置いてみる。
② 7を置くと1周してもとの位置に戻るので、7を置くのは最後。
③ 1~6までを置けたとすると、置いたときの数の和(1+2+3+4+5+6=)は21だから,3周してもとの位置(1の場所)に重なってしまう。
④よって,A=7の場合、1~7の数字を置くことはできない。
ちなみに、A=5やA=9の時も調べてみると、(重なりなく)置くことができません。
結局、「Aが奇数」の場合は重なることなく置くことができません。
これを一般化してみると、A=2n+1(=奇数)の場合は、直前の2nまで置いた時の和(Σ)=n×(2n+1)となります。
つまり、和(Σ)が”2n+1(=A)”のn倍になっていることになるので、(重なりなく)置くことは不可能となります。
例えば、n=50とすると、A=101となりますが、この場合は1~100まで置くと、n(50)周して「1」がある場所に戻ってしまうことになります。
小問(3)について
最後の小問(3)は、A=8の場合のすべての並びを書き出すのですが、これをもれなく書き出すことは、試験時間内では難しいかもしれません。それでも、前の結果を振り返れば、いくつかはすぐに書き出せます。そのあたりを、先生方は評価していらっしゃるのだと思います。
これは超難問です。
答えは4つあるようですが、1つでも書けたらすごいと思います。
A=8の場合ですが、A=6,A=7の考え方を生かして、8を置く直前の1~7までの数を置いたときの和を求めます。
すると、(1+2+3+4+5+6+7=)28となります。28÷8=3あまり4から、8は1の真向かいの位置にくることがわかります。
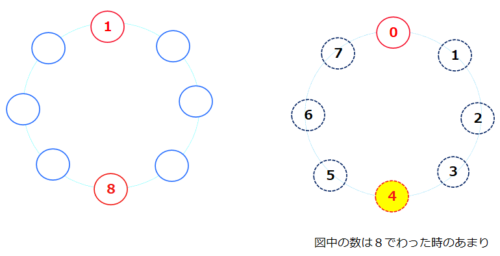
ここまで分かっても、この後の絞り込みが難しい。
剰余に注目して、「合同式(mod)を使えば効率的に求まるかな?」などと考えましたが、数字の並び順の候補を単純計算しただけで、200通りを超えそうです。
1+2,1+2+〇,1+2+〇+☆…とか、1+3,1+3+▢,1+3+▢+…などと足していって和を計算し、8でわったときの余りが0,1,4になったり(但し、最後に4になる場合はOK)、あまりが同じになったりするとNG、という感じで試行錯誤する方法しか思いつきません。
たまたま、小さい順に2→3→4→…と入れていったら1つは比較的簡単に見つかりましたが…。
この問題、系統的な方法(うまい方法)があるのでしょうか?
.png)

