本日の記事はこちら ↓


「11×11~19×19」を爆速で暗算できる おみやげ算とは?
さっそくですが、おみやげ算の計算法について説明します。
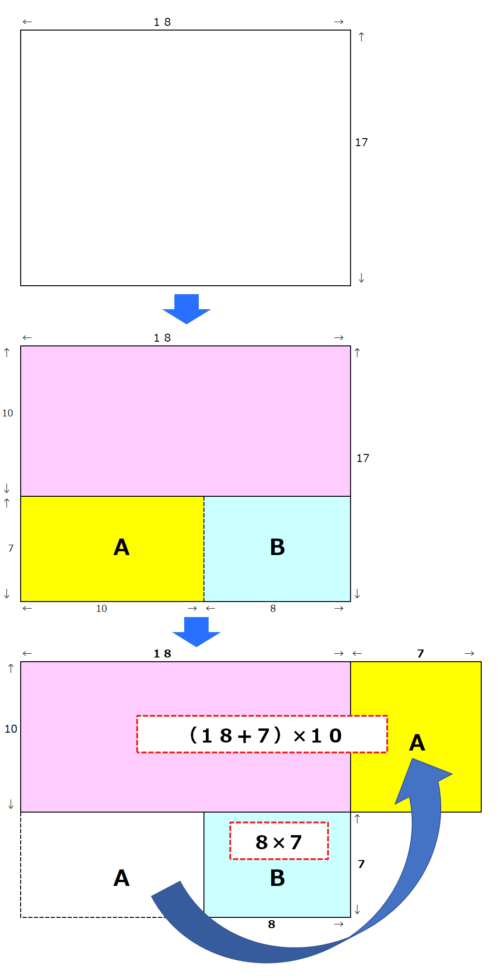
(例)18×17=
①18×17の右の「17の一の位の7」をおみやげとして、左の18に渡します。すると、18×17が、(18+7)×(17-7)=25×10(=250)になります。
②その250に、「18の一の位の8」と「おみやげの7」をかけた56をたした306が答えです。
まとめると、18×17=(18+7)×(17-7)+8×7=250+56=306です。
こうした計算を「おみやげ算」というのは初めて知りました。
文字だと今一つ伝わりにくいですが、「おみやげ算」の構造を図解で補足すると以下の通りとなります。
Aの図形を90°回転させて、くっつけるイメージですね。
確かに、(18+7)×10 + 8 × 7 =250+56=306となります。
おみやげ算を「覚える」必要があるか?
ただ、「おみやげ算」を覚える必要があると言われると、個人的にはやや疑問です。
というのも、「おみやげ算」の計算ロジックが使えるのは、(17×18とか24×27のような)十の位が同じ数同士のかけ算に限られるからです。その理由は、Aの部分を90度回転させてくっつけていることから明らかです。
「なぜこのような計算を行うことが可能なのか」ということを考えたり、「2けたかけ算の暗算ロジックについて、自分で色々考えてみる」というように、数を使った遊びはすることには大賛成なのですが、「計算方法」として覚える段になると、(私などは)一気に興味が薄れてしまいます。
さらに、①計算の正確性、②計算の速さの2つの点で筆算を上回るのであれば、こうした計算方法を覚える効用もあると思うのですが、(計算方法を覚えても)それほど「速く正確になる」とも思えません。
むしろ18×17であれば、例えば分配法則を使って、18×(10+7)=180+126=306、と計算した方が汎用性が高いような気がします。
算数に興味を持つ一つのきっかけに
ただ、計算方法を覚えることで精神的なゆとりは持つことはできるのは確かだと思います。また、面倒な筆算が瞬時に計算できるという喜びから、「算数が好きになる」という効用もあると思います。
なので、子供が興味を持って「おみやげ算を覚えたい」と思うのであれば、親としてサポートしてあげることには賛成です。


